
����Ŀ��ij��������һ��������Ԫ�������������������ͼ���ˮƽ�����ƣ������һЩ��Ʒ�����ݾ���֪�������Ʒ��P���ղ���x�������֮����������ϵ�� 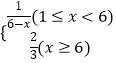 ����ע����Ʒ��=��Ʒ��/����������P=0.1��ʾÿ����10����Ʒ����1��Ϊ��Ʒ������Ϊ�ϸ�Ʒ������֪ÿ����1����ϸ��Ԫ������ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ���ʳ���ϣ���������ʵ��ղ�����
����ע����Ʒ��=��Ʒ��/����������P=0.1��ʾÿ����10����Ʒ����1��Ϊ��Ʒ������Ϊ�ϸ�Ʒ������֪ÿ����1����ϸ��Ԫ������ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ���ʳ���ϣ���������ʵ��ղ�����
��1���Խ���������������Ԫ��ÿ���ӯ����T����Ԫ����ʾΪ�ղ���x��������ĺ�����
��2�����ղ���xΪ����ʱ���ɻ���������
���𰸡�
��1���⣺��x��6ʱ��P= ![]() ����T=
����T= ![]() x��2��
x��2�� ![]() x��1=0��
x��1=0��
��1��x��6ʱ��P= ![]() ����T=��1��
����T=��1�� ![]() ��x��2����
��x��2���� ![]() ��x��1=
��x��1= ![]() ��
��
������������ӯ����T����Ԫ�����ղ���x��������ĺ�����ϵΪ��T= 
��2���⣺�ɣ�1��֪����x��6ʱ��ÿ���ӯ��Ϊ0��
��1��x��6ʱ��T��x��= ![]() =15��2[��6��x��+
=15��2[��6��x��+ ![]() ]��15��12=3��
]��15��12=3��
��T��3��
���ҽ���x=3ʱ��T=3��
���ϣ����ղ���Ϊ3���ʱ���ɻ���������3��Ԫ
����������1��ÿ���Ӯ��ΪT=�ղ�����x������Ʒ�ʣ�1��P����2���ղ�����x������Ʒ�ʣ�P����1�����ݷֶκ����ֶ��о����������ɣ���2�����û�������ʽ���������ֵ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=f��x���Ķ�����ΪR����x��0ʱ��f��x����1���Ҷ������ʵ��x��y��R����ʽf��x��f��y��=f��x+y��������������{an}���� ![]() ����n��N*������a1=f��0���������н��۳������ǣ� ��
����n��N*������a1=f��0���������н��۳������ǣ� ��
A.f��a2013����f��a2016��
B.f��a2014����f��a2015��
C.f��a2016����f��a2015��
D.f��a2014����f��a2016��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �붨��
�붨��![]() �ľ��������ֱ��
�ľ��������ֱ��![]() �ľ���ı��dz���
�ľ���ı��dz���![]() ��
��
��1�����![]() �Ĺ켣����
�Ĺ켣����![]() �ķ��̣�
�ķ��̣�
��2��������![]() ��ֱ��
��ֱ��![]() ������
������![]() ��
��![]() ���㣬��
���㣬��![]() ���㣨
���㣨![]() Ϊ����ԭ�㣩Ϊ������ƽ���ı���
Ϊ����ԭ�㣩Ϊ������ƽ���ı���![]() ,����
,����![]() �պ�������
�պ�������![]() �ϣ���ֱ��
�ϣ���ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������Ϊ�����Σ������ڵ����ϵ���Ӱ�ǵ�������ģ�S��ABCD�ĵ���߳�Ϊ2����Ϊ2��EΪ��BC���е㣬����P�ڱ������˶��������ܱ���PE��AC����P�Ĺ켣���ܳ�Ϊ�� ��
A.![]()
B.![]()
C.3 ![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݹ��һ����������ġ������������������涨��������![]() ����ƽ��Ũ�Ȳ��ó���35��/�����ף�
����ƽ��Ũ�Ȳ��ó���35��/�����ף� ![]() ��24Сʱƽ��Ũ�Ȳ��ó���75��/�����ף����л����������ȡ��һ������2016��30��
��24Сʱƽ��Ũ�Ȳ��ó���75��/�����ף����л����������ȡ��һ������2016��30��![]() ��24Сʱƽ��Ũ�ȣ���λ����/�����ף��ļ�����ݣ�����30��IJ���������Ƴ�����Ƶ�ʷֲ�ֱ��ͼ��ͼ��
��24Сʱƽ��Ũ�ȣ���λ����/�����ף��ļ�����ݣ�����30��IJ���������Ƴ�����Ƶ�ʷֲ�ֱ��ͼ��ͼ��
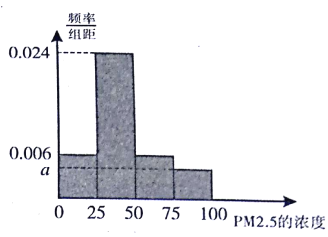
������ͼ��![]() ��ֵ��
��ֵ��
������Ƶ�ʷֲ�ֱ��ͼ�й�������ƽ�������������������������˼�룬��![]() ����ƽ��Ũ�ȿ��ǣ��жϸþ������Ļ��������Ƿ���Ҫ���ƣ���˵�����ɣ�
����ƽ��Ũ�ȿ��ǣ��жϸþ������Ļ��������Ƿ���Ҫ���ƣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���뾶Ϊ![]() ��Բ��ֽ������һ����ͬԲ�ĵİ뾶Ϊ
��Բ��ֽ������һ����ͬԲ�ĵİ뾶Ϊ![]() ��СԲ���ֽ��뾶Ϊ
��СԲ���ֽ��뾶Ϊ![]() ��һöӲ������ֽ���ϣ�ʹ����Ӳ����ȫ�������ֽ���ڣ���Ӳ����СԲ������ĸ���Ϊ�� ��
��һöӲ������ֽ���ϣ�ʹ����Ӳ����ȫ�������ֽ���ڣ���Ӳ����СԲ������ĸ���Ϊ�� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����������ijУ20���༶����������ע������д������ѧ�������������������ݵľ�Ҷͼ�������Ϊ5�����ݷ����[0��5����[5��10����[10��15����[15��20����[20��25����[25��30����[30��35����[35��40]ʱ��������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����ԭʼ��Ҷͼ�����ǣ� �� 
A.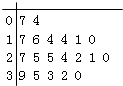
B.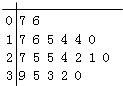
C.
D.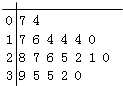
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������̾���ij��ũ��Ʒ����һ�����ۼ����ڣ�ÿ�۳�![]() �ò�Ʒ������500Ԫ��δ�۳��IJ�Ʒ��ÿ
�ò�Ʒ������500Ԫ��δ�۳��IJ�Ʒ��ÿ![]() ����300Ԫ��������ʷ���ϣ��õ����ۼ������г���������Ƶ�ʷֲ�ֱͼ����ͼ��ʾ��������Ϊ��һ�����ۼ��ȹ�����
����300Ԫ��������ʷ���ϣ��õ����ۼ������г���������Ƶ�ʷֲ�ֱͼ����ͼ��ʾ��������Ϊ��һ�����ۼ��ȹ�����![]() ��ũ��Ʒ����
��ũ��Ʒ����![]() ��
��![]() ����ʾ��һ�����ۼ����ڵ��г���������
����ʾ��һ�����ۼ����ڵ��г��������� ![]() ����λ��Ԫ����ʾ��һ�����ۼ����ھ�����ũ��Ʒ������
����λ��Ԫ����ʾ��һ�����ۼ����ھ�����ũ��Ʒ������
����![]() ��ʾΪ
��ʾΪ![]() �ĺ�����
�����
������ֱ��ͼ��������![]() ������57000Ԫ�ĸ��ʣ�
������57000Ԫ�ĸ��ʣ�
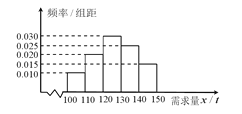
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ֱ��![]() ����
����![]() ������Բ
������Բ![]() ����
����![]() ��
��![]() ���㣮
���㣮
��1����ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ����
����![]() �������
�������
��2����ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ����
����![]() ��Բ
��Բ![]() ������һ�㣬��
������һ�㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���Ƿ����һ������![]() ����ͬ�ڵ�
����ͬ�ڵ�![]() �����������ⲻ��
�����������ⲻ��![]() ���غϵ�ֱ��
���غϵ�ֱ��![]() ������
������![]() ƽ��
ƽ��![]() �������ڣ��������
�������ڣ��������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com