
【题目】如图,已知动直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的面积;
的面积;
(2)若直线![]() 的斜率为
的斜率为![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,求
上任意一点,求![]() 的取值范围;
的取值范围;
(3)是否存在一个定点![]() (不同于点
(不同于点![]() ),对于任意不与
),对于任意不与![]() 轴重合的直线
轴重合的直线![]() ,都有
,都有![]() 平分
平分![]() ,若存在,求出定点
,若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:
(1)利用题意分别求得距离和弦长可得![]() ;
;
(2)利用题意得到关于纵坐标y的函数,结合定义域可得![]() 的取值范围是
的取值范围是![]() .
.
(3)联立直线和圆的方程,结合对称性可得点Q存在,其坐标为![]() .
.
试题解析:
解:(1)因为直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]()
![]() ,
,
则点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以弦![]() 的长度
的长度![]() ,
,
所以![]() .
.
(2)因为直线![]() 的斜率为
的斜率为![]() ,所以可知
,所以可知![]() 、
、![]() ,
,
设点![]() ,则
,则![]() ,
,
又![]() ,
,
所以![]() ,又
,又![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.
(3)法一: 若存在,则根据对称性可知,定点![]() 在
在![]() 轴上,设
轴上,设![]() 、又设
、又设![]() 、
、![]() ,
,
因直线![]() 不与
不与![]() 轴重合,设直线
轴重合,设直线![]()
![]() ,
,
代入圆![]() 得
得![]() ,
,
所以![]() (*)
(*)
若![]() 平分
平分![]() ,则根据角平分线的定义,
,则根据角平分线的定义,![]() 与
与![]() 的斜率互为相反数
的斜率互为相反数
有![]() ,又
,又![]() ,
,![]() ,
,
化简可得![]() ,
,
代入(*)式得![]() ,因为直线
,因为直线![]() 任意,故
任意,故![]() ,
,
即![]() , 即
, 即![]()
解法二:若存在,则根据对称性可知,定点![]() 在
在![]() 轴上,设
轴上,设![]() 、又设
、又设![]() 、
、![]() ,
,
因直线![]() 不与
不与![]() 轴重合,设直线
轴重合,设直线![]()
![]() ,
,
代入圆![]() 得
得![]() ,
,
所以![]() (*)
(*)
若![]() 平分
平分![]() ,则根据角平分线的几何意义,点
,则根据角平分线的几何意义,点![]() 到
到![]() 轴的距离
轴的距离![]() ,点
,点![]() 到
到![]() 轴的距离
轴的距离![]() 满足
满足![]() ,即
,即![]() ,
,
化简可得![]() ,
,
代入(*)式得![]() ,因为直线
,因为直线![]() 任意,故
任意,故![]() ,
,
即![]() , 即
, 即![]()


科目:高中数学 来源: 题型:
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系: 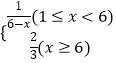 .(注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品).已知每生产1万件合格的元件可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
.(注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品).已知每生产1万件合格的元件可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量x为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该分店此次抽奖活动自开业始,持续![]() 天,参加抽奖的每位顾客抽到一等奖(价值
天,参加抽奖的每位顾客抽到一等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() ,抽到二等奖(价值
,抽到二等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() ,抽到三等奖(价值
,抽到三等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() .
.
试估计该分店在此次抽奖活动结束时送出多少元奖品?
参考公式: 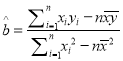 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=2sin(﹣2x+ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位后,得到的图象对应的解析式应该是( )
个单位后,得到的图象对应的解析式应该是( )
A.y=﹣2sin(2x)
B.y=﹣2sin(2x+ ![]() )
)
C.y=﹣2sin(2x﹣ ![]() )
)
D.y=﹣2sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【河北省衡水中学2017届高三上学期五调】已知椭圆![]() ,圆
,圆![]() 的圆心
的圆心![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 到椭圆
到椭圆![]() 的右焦点的距离为
的右焦点的距离为![]() .
.
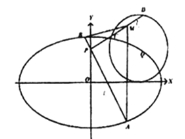
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,且
,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 交圆
交圆![]() 于
于![]() 两点,且
两点,且![]() 为
为![]() 的中点,求
的中点,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程是
的参数方程是 (
(![]() 是参数),以坐标原点为原点,
是参数),以坐标原点为原点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)过直线![]() 上的点作曲线
上的点作曲线![]() 的切线,求切线长的最小值.
的切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 上顶点为
上顶点为![]() ,右顶点为
,右顶点为![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 过点
过点![]() ,直线
,直线![]() 与圆
与圆![]() 相交得到的弦长为
相交得到的弦长为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,
两点, ![]() 与
与![]() 轴,
轴, ![]() 轴分别相交于
轴分别相交于![]() 两点,满足:①记
两点,满足:①记![]() 的中点为
的中点为![]() ,且
,且![]() 两点到直线
两点到直线![]() 的距离相等;②记
的距离相等;②记![]() 的面积分别为
的面积分别为![]() 若
若![]() 当
当![]() 取得最大值时,求
取得最大值时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com