
 ,
,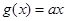 ,
,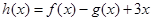 ,其中
,其中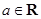 且
且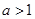 .
.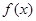 的导函数
的导函数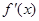 的最小值;
的最小值;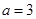 时,求函数
时,求函数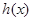 的单调区间及极值;
的单调区间及极值;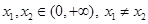 ,函数
,函数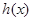 满足
满足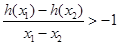 ,求实数
,求实数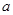 的取值范围.
的取值范围.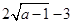 ;(II)单调增区间是
;(II)单调增区间是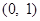 ,
, ;单调减区间是
;单调减区间是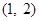 ;
;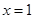 处取得极大值
处取得极大值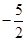 ,在
,在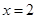 处取得极小值
处取得极小值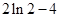 .(III)
.(III)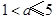 。
。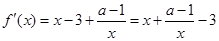 ,其中
,其中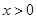 .
.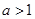 ,所以
,所以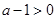 ,又
,又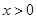 ,所以
,所以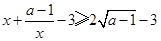 ,
,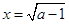 时取等号,其最小值为
时取等号,其最小值为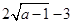 . 2……………………4分
. 2……………………4分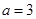 时,
时,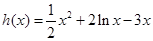 ,
,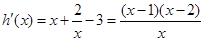 .…5分
.…5分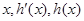 的变化如下表:
的变化如下表: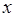 | 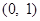 | 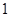 | 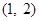 | 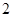 |  |
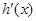 | 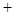 | 0 | 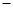 | 0 | 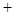 |
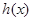 |  | 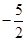 |  | 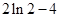 |  |
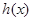 的单调增区间是
的单调增区间是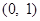 ,
, ;单调减区间是
;单调减区间是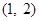 .……7分
.……7分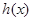 在
在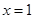 处取得极大值
处取得极大值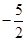 ,在
,在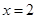 处取得极小值
处取得极小值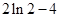 .……8分
.……8分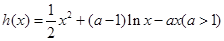 .
.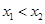 ,则由
,则由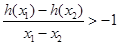 得
得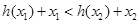 .
. 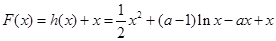 ,则函数
,则函数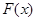 在
在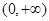 单调递增.10分
单调递增.10分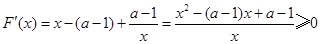 在
在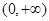 恒成立.
恒成立.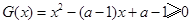 在
在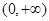 恒成立.
恒成立.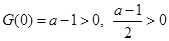 ,因此,只需
,因此,只需 .
.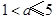 . 故所求实数
. 故所求实数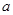 的取值范围为
的取值范围为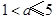 . …12分
. …12分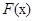 ,把证明
,把证明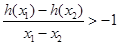 转化为证明
转化为证明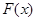 在
在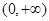 单调递增是做本题的关键,运用了转化思想,对学生的能力要求较高,是一道中档题。
单调递增是做本题的关键,运用了转化思想,对学生的能力要求较高,是一道中档题。

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 。
。 ,而使得不等式
,而使得不等式 能成立,求实数
能成立,求实数 的最小值;
的最小值; 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围。
的取值范围。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com