
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=SB,点M是SD的中点,AN⊥SC,且交SC于点N. 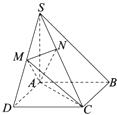
(1)求证:SC⊥平面AMN;
(2)求二面角D﹣AC﹣M的余弦值.
【答案】
(1)证明:∵在四棱锥S﹣ABCD中,底面ABCD是正方形,SA⊥底面ABCD,
∴以A为坐标原点,AD为x轴,AB为y轴,AS为z轴,建立空间直角坐标系,
由SA=AB,设AB=AD=AS=1,
则A(0,0,0),B(0,1,0),C(1,1,0),D(1,0,0),S(0,0,1),M( ![]() ,0,
,0, ![]() ),
),
![]() =(
=( ![]() ,0,
,0, ![]() ),
), ![]() =(﹣1,﹣1,1),
=(﹣1,﹣1,1),
![]()
![]() =﹣
=﹣ ![]() +
+ ![]() =0,∴
=0,∴ ![]() ,
,
∴SC⊥⊥AM,
又SC⊥AN,且AN∩AM=A,
∴SC⊥平面AMN
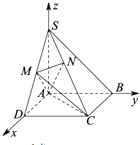
(2)解:∵SA⊥底面ABCD,∴ ![]() 是平面ABCD的一个法向量,且
是平面ABCD的一个法向量,且 ![]() =(0,0,1),
=(0,0,1),
设平面ACM的法向量为 ![]() =(x,y,z),
=(x,y,z),
![]() =(1,1,0),
=(1,1,0), ![]() =(
=( ![]() ,0,
,0, ![]() ),
),
则 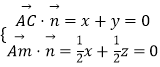 ,取x=﹣1,得
,取x=﹣1,得 ![]() =(﹣1,1,1),
=(﹣1,1,1),
cos< ![]() ,
, ![]() >=
>= 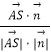 =
= ![]() =
= ![]() ,
,
由图形知二面角D﹣AC﹣M为锐二面角,
∴二面角D﹣AC﹣M的余弦值为 ![]()
【解析】(1)以A为坐标原点,AD为x轴,AB为y轴,AS为z轴,建立空间直角坐标系,利用向量法能证明SC⊥平面AMN.(2)求出平面ABCD的一个法向量和平面ACM的法向量,利用向量法能求出二面角D﹣AC﹣M的余弦值.
【考点精析】认真审题,首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想).


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=2sin(2x+ ![]() ),g(x)=mcos(2x﹣
),g(x)=mcos(2x﹣ ![]() )﹣2m+3(m>0),若对任意x1∈[0,
)﹣2m+3(m>0),若对任意x1∈[0, ![]() ],存在x2∈[0,
],存在x2∈[0, ![]() ],使得g(x1)=f(x2)成立,则实数m的取值范围是( )
],使得g(x1)=f(x2)成立,则实数m的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2 ![]() ,(其中,t为关税的税率,且t∈[0,
,(其中,t为关税的税率,且t∈[0, ![]() ),x为市场价格,b,k为正常数),当t=
),x为市场价格,b,k为正常数),当t= ![]() 时的市场供应量曲线如图.
时的市场供应量曲线如图. 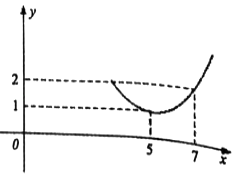
(Ⅰ)根据图象求b,k的值;
(Ⅱ)若市场需求量为Q(x)=2 ![]() ,当p=Q时的市场价格称为市场平衡价格,当市场平衡价格保持在10元时,求税率t的值.
,当p=Q时的市场价格称为市场平衡价格,当市场平衡价格保持在10元时,求税率t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是A,B,C的对边,且2cosA= ![]() .
.
(1)若a2﹣c2=b2﹣mbc,求实数m的值;
(2)若a=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,若∠BAC=90°,AB=AC=AA1 , 则异面直线BA1与AC1所成的角等于( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水利工程队相应政府号召,计划在韩江边选择一块矩形农田,挖土以加固河堤,为了不影响农民收入,挖土后的农田改造成面积为32400m2的矩形鱼塘,其四周都留有宽3m的路面,问所选的农田的长和宽各为多少时,才能使占有农田的面积最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC.设AB=2. 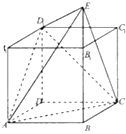
(1)求二面角E﹣AC﹣D1的大小;
(2)在D1E上是否存在一点P,使A1P∥面EAC?若存在,求D1P:PE的值;不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为 ![]() ,BC=
,BC= ![]() ,AC=1,∠ACB=90°,则此球的体积等于( )
,AC=1,∠ACB=90°,则此球的体积等于( )
A.![]() π
π
B.![]() π
π
C.![]() π
π
D.8π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com