
 如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.
如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.分析 (Ⅰ)连结BC1,B1C连结DE,可得DE∥AB,即可得AB∥平面CDB1;
(Ⅱ)(1)可得BC⊥CD,在RtBCD中,由BC=1,CD=$\frac{1}{2}A{C}_{1}$=$\frac{1}{2}\sqrt{A{C}^{2}+C{{C}_{1}}^{2}}$=1,可得BD
(2)V${\;}_{C-D{B}_{1}{C}_{1}}$=V${\;}_{{B}_{1}-CD{C}_{1}}$=$\frac{1}{2}{S}_{△CD{C}_{1}}•{B}_{1}{C}_{1}$=$\frac{1}{3}×\frac{1}{4}×1×\sqrt{3}×1=\frac{\sqrt{3}}{12}$
解答 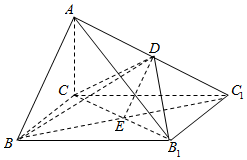 解:(Ⅰ)证明:连结BC1,B1C连结DE,--------------------------(1分)
解:(Ⅰ)证明:连结BC1,B1C连结DE,--------------------------(1分)
∵D、E分别为AC1,BC1,∴DE∥AB,-------------------------------(2分)
又∵DE?CDB1 AB?CDB1,∴AB∥平面CDB1;---------------------------------(4分)
(Ⅱ)(1)∵AC⊥平面BCC1B1,BC?BCC1B1
∴BC⊥AC
∵BC⊥CC1,AC∩CC1=C
BC⊥平面ACC1,CD?平面ACC1
∴BC⊥CD------------------------------------------------------------------------------(6分)
在R△BCD中,∵BC=1,CD=$\frac{1}{2}A{C}_{1}$=$\frac{1}{2}\sqrt{A{C}^{2}+C{{C}_{1}}^{2}}$=1
∴$BD=\sqrt{2}$--------------------------------------------------(8分)
(2)∵BC⊥平面ACC1,BC∥B1C1
∴B1C1⊥平面ACC1,-----------------------------------------------------------------------------------------(10分)
∴V${\;}_{C-D{B}_{1}{C}_{1}}$=V${\;}_{{B}_{1}-CD{C}_{1}}$=$\frac{1}{2}{S}_{△CD{C}_{1}}•{B}_{1}{C}_{1}$=$\frac{1}{3}×\frac{1}{4}×1×\sqrt{3}×1=\frac{\sqrt{3}}{12}$-----------------------------(12分)
点评 本题考查了空间位置关系的判定,几何体体积的计算,属于中档题.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=2|x+1|-|x-2|,x∈[-3,3].
已知函数f(x)=2|x+1|-|x-2|,x∈[-3,3].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com