
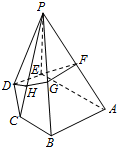
 如图所示,在五棱锥P-ABCDE中,PE⊥平面ABCDE,DE⊥AE,AB∥DE,BC∥AE.AE=AB=PE=2DE=2BC,F为棱PA的中点,过D、E、F的平面α与棱PB、PC分别交于点G、H.
如图所示,在五棱锥P-ABCDE中,PE⊥平面ABCDE,DE⊥AE,AB∥DE,BC∥AE.AE=AB=PE=2DE=2BC,F为棱PA的中点,过D、E、F的平面α与棱PB、PC分别交于点G、H.分析 (1)利用线面平行的判定与性质,证明DE∥FG;
(2)由(1)知,F为棱PA的中点,G为棱PB的中点,利用三棱锥G-PEF的体积=$\frac{1}{2}$VB-PEF=$\frac{1}{2}×\frac{1}{2}×{V}_{B-PEA}$=$\frac{1}{4}×{V}_{P-BEA}$,即可求三棱锥G-PEF的体积.
解答 (1)证明:∵AB∥DE,AB?平面PAB,DE?平面PAB,
∴DE∥平面PAB,
∵DE?α,α∩平面PAB=FG,
∴DE∥FG;
(2)解:由(1)知,F为棱PA的中点,G为棱PB的中点,
∴三棱锥G-PEF的体积=$\frac{1}{2}$VB-PEF=$\frac{1}{2}×\frac{1}{2}×{V}_{B-PEA}$=$\frac{1}{4}×{V}_{P-BEA}$=$\frac{1}{4}×\frac{1}{3}{S}_{△BEA}×PE$
=$\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{1}{3}$.
点评 本题考查线面平行的判定与性质,考查三棱锥G-PEF的体积,正确运用线面平行的判定与性质是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知P为△ABC所在平面外一点,G1、G2、G3分别是△PAB、△PCB、△PAC的重心;D、E、F分别是AB、BC、CA的中点.
已知P为△ABC所在平面外一点,G1、G2、G3分别是△PAB、△PCB、△PAC的重心;D、E、F分别是AB、BC、CA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱 ABC-A1 B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱 ABC-A1 B1C1中,CA=CB,AB=AA1,∠BAA1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
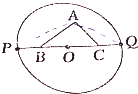 如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.
如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}{x,x∈[0,2]}\\{\frac{4}{x},x∈(2,4]}\end{array}\right.$
已知函数f(x)=$\left\{\begin{array}{l}{x,x∈[0,2]}\\{\frac{4}{x},x∈(2,4]}\end{array}\right.$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com