
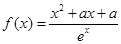 ,其
,其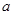 中为常数,
中为常数,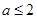 .
.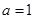 时,求曲线
时,求曲线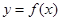 在点
在点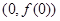 处的切线方程;
处的切线方程;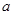 ,使
,使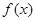 的极大值为
的极大值为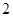 ?若存在,求出
?若存在,求出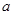 的值;若不存在,说明理由.
的值;若不存在,说明理由.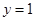 ;(2)不存在.
;(2)不存在.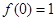 ,而曲线在点
,而曲线在点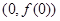 处的切线的斜率为
处的切线的斜率为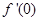 ,因此先求导数,
,因此先求导数,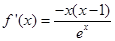 ,得
,得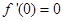 ,故切线方程为
,故切线方程为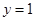 ;(2)这种存在性命题都是先假设存在,然后去求参数
;(2)这种存在性命题都是先假设存在,然后去求参数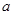 的值,如能求得,则存在,如求不出,说明假设错误,结论就是不存在,利用导数公式可得
的值,如能求得,则存在,如求不出,说明假设错误,结论就是不存在,利用导数公式可得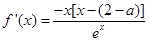 ,极值点是使
,极值点是使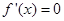 的点,本题中可得
的点,本题中可得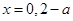 ,由于已知条件是
,由于已知条件是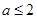 ,可分类讨论,
,可分类讨论,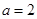 时,
时,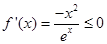 在
在 上恒成立,即
上恒成立,即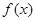 在
在 上单调递减,无极值,当
上单调递减,无极值,当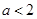 时,
时,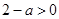 ,通过讨论
,通过讨论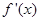 在
在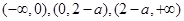 上的符号,确定出
上的符号,确定出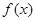 的单调性,也即确定出极大值点有
的单调性,也即确定出极大值点有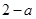 ,极大值为
,极大值为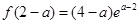 ,接下来考虑的是
,接下来考虑的是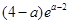 能否等于2,解方程
能否等于2,解方程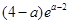
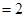 是不可能的(可以猜测计算出
是不可能的(可以猜测计算出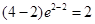 ),可讨论函数
),可讨论函数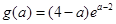 的单调性,确定其值域或最值。
的单调性,确定其值域或最值。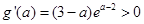 ,因此
,因此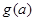 在
在 单调递增,从而
单调递增,从而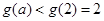 ,故
,故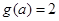 无解,
无解,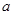 不存在.
不存在.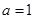 ,
,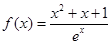 ,
,
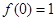 , 1分
, 1分
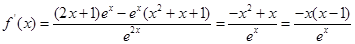 ,
,
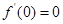 3分
3分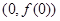 处的切线方程为
处的切线方程为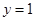 . 5分
. 5分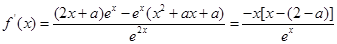
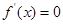 的根为
的根为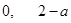 , 6分
, 6分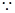
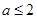 ,
,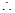

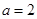 时,
时,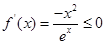 ,
,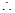
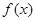 在
在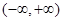 递减,无极值; 8分
递减,无极值; 8分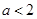 时,
时,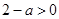 ,
,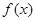 在
在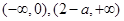 递减,在
递减,在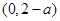 递增;
递增;
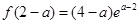 为
为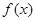 的极大值, 10分
的极大值, 10分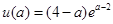 ,
,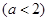 ,
,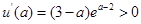
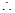
 在
在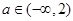 上递增,
上递增,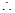
 ,
,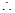 不存在实数
不存在实数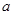 ,使
,使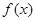 的极大值为
的极大值为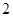 . 13分
. 13分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
A.命题“存在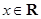 , ,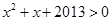 ”的否定是“任意 ”的否定是“任意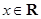 , ,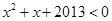 ” ” |
| B.两个三角形全等是这两个三角形面积相等的必要条件 |
C.函数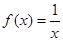 在其定义域上是减函数 在其定义域上是减函数 |
D.给定命题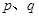 ,若“ ,若“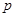 且 且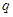 ”是真命题,则 ”是真命题,则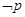 是假命题 是假命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com