
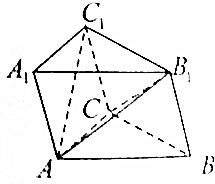
 如图所示,三棱柱ABC-A1B1C1的所有棱长都相等,∠C1CB=120°.
如图所示,三棱柱ABC-A1B1C1的所有棱长都相等,∠C1CB=120°.分析 (1)由题意可知△ABC,△CBB1是正三角形,取BC的中点D,连结B1D,AD,则BC⊥AD,BC⊥B1D,于是BC⊥平面AB1D,从而BC⊥AB1;
(2)设AB=1,求出AD,B1D,根据勾股定理的逆定理得出AD⊥B1D,于是B1D⊥平面ABC,以D为坐标原点建立空间坐标系,求出平面AB1C和平面AB1C1的法向量,则法向量夹角的余弦值的绝对值为二面角的余弦值.
解答 解: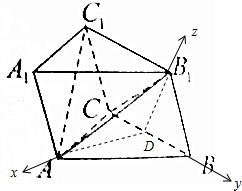 (1)BC⊥AB1,证明如下:
(1)BC⊥AB1,证明如下:
∵三棱柱的所有棱长都相等,∠C1CB=120°,
∴△ABC,△CBB1是正三角形,
取BC的中点D,连结B1D,AD,
则AD⊥BC,B1D⊥BC,又AD?平面AB1D,B1D?平面AB1D,AD∩B1D=D,
∴BC⊥平面AB1D,又AB1?平面AB1D,
∴BC⊥AB1.
(2)设AB=1,则AD=B1D=$\frac{\sqrt{3}}{2}$,
∵AB1=$\frac{\sqrt{6}}{2}AB$=1,
∴AD2+B1D2=AB12,∴AD⊥B1D,
又B1D⊥BC,AD?平面ABC,BC?平面ABC,AD∩BC=D,
∴B1D⊥平面ABC.
以D为坐标原点,建立如图所示的空间直角坐标系,
则A($\frac{\sqrt{3}}{2}$,0,0),B1(0,0,$\frac{\sqrt{3}}{2}$),C(0,-$\frac{1}{2}$,0),C1(0,-1,$\frac{\sqrt{3}}{2}$).
∴$\overrightarrow{A{B}_{1}}$=(-$\frac{\sqrt{3}}{2}$,0,$\frac{\sqrt{3}}{2}$),$\overrightarrow{AC}$=(-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,0),$\overrightarrow{A{C}_{1}}$=(-$\frac{\sqrt{3}}{2}$,-1,$\frac{\sqrt{3}}{2}$).
设平面AB1C的法向量为$\overrightarrow{{n}_{1}}$=(x,y,z),平面AB1C1的法向量为$\overrightarrow{{n}_{2}}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{A{B}_{1}}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{AC}=0}\end{array}\right.$,$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}•\overrightarrow{A{B}_{1}}=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{A{C}_{1}}=0}\end{array}\right.$.
∴$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{2}x+\frac{\sqrt{3}}{2}z=0}\\{-\frac{\sqrt{3}}{2}x-\frac{1}{2}y=0}\end{array}\right.$,$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{2}a+\frac{\sqrt{3}}{2}c=0}\\{-\frac{\sqrt{3}}{2}a-b+\frac{\sqrt{3}}{2}c=0}\end{array}\right.$.
令z=1得$\overrightarrow{{n}_{1}}$=(1,-$\sqrt{3}$,1),令c=1得$\overrightarrow{{n}_{2}}$=(1,0,1).
∴$\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}$=2,|$\overrightarrow{{n}_{1}}$|=$\sqrt{5}$,|$\overrightarrow{{n}_{2}}$|=$\sqrt{2}$.
∴cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{\sqrt{10}}{5}$.
∴二面角C-AB1-C1的余弦值为$\frac{\sqrt{10}}{5}$.
点评 本题考查了线面垂直的判定与性质,空间向量在立体几何中的应用,属于中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-i | B. | 2+i | C. | 4-i | D. | 4+i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com