
分析 (1)求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)把方程化为 $\frac{lnx}{x}$=x2-2ex+a,求得 h(x)=$\frac{lnx}{x}$的最大值为 h(e)=$\frac{1}{e}$,再求得m(x)=x2-2ex+a 的最小值 m(e)=a-e2,根据 a-e2=$\frac{1}{e}$求出a的值.
解答 解:(1)函数f(x)的定义域是(0,+∞),
a=2时,f(x)=x+$\frac{2}{x}$+lnx,f′(x)=1-$\frac{2}{{x}^{2}}$+$\frac{1}{x}$=$\frac{(x+2)(x-1)}{{x}^{2}}$,
令f′(x)>0,解得:x>1,令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)递减,在(1,+∞)递增;
(2)关于x的方程g(x)=$\frac{lnx}{{x}^{2}}$-f(x)+lnx+2e,可化为 $\frac{lnx}{x}$=x2-2ex+a,
令h(x)=$\frac{lnx}{x}$,令h′(x)=0,得x=e,故 h(x)的最大值为 h(e)=$\frac{1}{e}$.
令m(x)=x2-2ex+a,可得:x=e时,m(x)的最小值 m(e)=a-e2 ,
由 a-e2=$\frac{1}{e}$可得 a=e2+$\frac{1}{e}$.
点评 本题主要考查导数的运算法则的应用,利用导数求函数的单调区间、最值问题,体现了转化的数学思想,属于中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:解答题
 2016年里约奥运会和残奥会吉祥物的名字于2015年12月14日揭晓,两个吉祥物分别叫维尼修斯(Vinicius)和汤姆(Tom)(如图),以此纪念巴萨诺瓦曲风的著名音乐家Viniciusde Moraes和Tom Jobim.某商场在抽奖箱中放置了除图案外,其它无差别的8张卡片,其中2张印有“维尼修斯(Vinicius)”图案,n(2≤n≤4)张印有“汤姆(Tom)”图案,其余卡片上印有“2016年里约奥运会”的图案,
2016年里约奥运会和残奥会吉祥物的名字于2015年12月14日揭晓,两个吉祥物分别叫维尼修斯(Vinicius)和汤姆(Tom)(如图),以此纪念巴萨诺瓦曲风的著名音乐家Viniciusde Moraes和Tom Jobim.某商场在抽奖箱中放置了除图案外,其它无差别的8张卡片,其中2张印有“维尼修斯(Vinicius)”图案,n(2≤n≤4)张印有“汤姆(Tom)”图案,其余卡片上印有“2016年里约奥运会”的图案,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
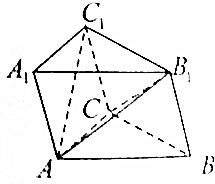 如图所示,三棱柱ABC-A1B1C1的所有棱长都相等,∠C1CB=120°.
如图所示,三棱柱ABC-A1B1C1的所有棱长都相等,∠C1CB=120°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com