
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 法一、充分性:在单位圆中,|PB|=sinx,$\widehat{PA}$=x,|AQ|=tanx,由于△POA的面积小于扇形POA的面积,扇形POA的面积小于△AOQ的面积,可得|PB|<$\widehat{PA}$<|AQ|,化简可得sinx<x<tanx,举反例说明不必要;
法二、构造函数,通过导数说明当0<x<$\frac{π}{2}$时,有sinx<x<tanx;举例说明当sinx<x<tanx时,不一定有0<x<$\frac{π}{2}$.
解答 解:法一、如图,当0<x<$\frac{π}{2}$时,
设角x的终边与单位圆的交点为P,作PB⊥x轴,B为垂足,
单位圆和x轴的正半轴交于点A,作AQ⊥x轴,且点Q∈OP,
如图所示,则|PB|=sinx,$\widehat{PA}$=x,|AQ|=tanx,
由于△POA的面积小于扇形POA的面积,扇形POA的面积小于△AOQ的面积,
故有$\frac{1}{2}$|OA|•|PB|<$\frac{1}{2}$$\widehat{PA}$•|OA|<$\frac{1}{2}$|OA|•|AQ|,
即|PB|<$\widehat{PA}$<|AQ|,即 sinx<x<tanx.
反之,若sinx<x<tanx,不一定有0<x<$\frac{π}{2}$,
如当x小于$\frac{3π}{2}$且无限接近于$\frac{3π}{2}$时,sinx<0,tanx→+∞,满足sinx<x<tanx,
但不满足0<x<$\frac{π}{2}$.
∴p是q的充分不必要条件.
法二、当0<x<$\frac{π}{2}$时,令f(x)=x-sinx,g(x)=tanx-x,
则f′(x)=1-cosx>0,g′(x)=$\frac{1}{co{s}^{2}x}$-1>0,
故f(x)和g(x)在(0,$\frac{π}{2}$)上单调递增,
∴f(x)>f(0)=0,g(x)>g(0)=0,
∴x>sinx,且tanx>x,∴sinx<x<tanx;
反之,若sinx<x<tanx,不一定有0<x<$\frac{π}{2}$,
如当x小于$\frac{3π}{2}$且无限接近于$\frac{3π}{2}$时,sinx<0,tanx→+∞,满足sinx<x<tanx,
但不满足0<x<$\frac{π}{2}$.
∴p是q的充分不必要条件.
故选:A.
点评 本题考查必要条件、充分条件与充要条件的判断方法,考查学生对三角函数线的理解,训练了利用导数研究函数的单调性,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | x-y-4=0 | B. | x-y+3=0 | C. | x+y-5=0 | D. | x+4y-17=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
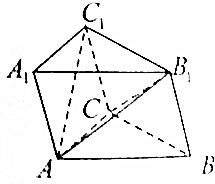 如图所示,三棱柱ABC-A1B1C1的所有棱长都相等,∠C1CB=120°.
如图所示,三棱柱ABC-A1B1C1的所有棱长都相等,∠C1CB=120°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -3 | C. | -2 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com