
已知点(1, )是函数f(x)=ax(a>0,且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=
)是函数f(x)=ax(a>0,且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=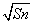 +
+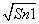 (n≥2).
(n≥2).
(1)求数列{an}和{bn}的通项公式;
(2)若数列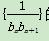 的前n项和为Tn,问满足Tn>
的前n项和为Tn,问满足Tn>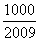 的最小正整数n是多少?
的最小正整数n是多少?
解 (1)因为f(1)=a= ,所以f(x)=
,所以f(x)=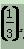 .
.
a1=f(1)-c= -c,a2=[f(2)-c]-[f(1)-c]=f(2)-f(1)=
-c,a2=[f(2)-c]-[f(1)-c]=f(2)-f(1)=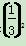 -
- =-
=-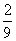 ,
,
a3=[f(3)-c]-[f(2)-c]=f(3)-f(2)=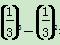 =-
=-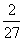 .
.
又数列{an}是等比数列,设其公比为q,所以a1=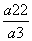 =
= =-
=-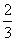 =
= -c,所以c=1.
-c,所以c=1.
又公比q= =
= ,
,
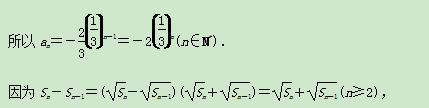 又bn>0,
又bn>0,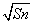 >0,所以
>0,所以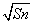 -
-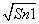 =1.
=1.
所以数列{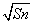 }构成一个首项为1,公差为1的等差数列,
}构成一个首项为1,公差为1的等差数列,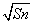 =1+(n-1)×1=n,故Sn=n2.
=1+(n-1)×1=n,故Sn=n2.
当n≥2时,bn=Sn-Sn-1=n2-(n-1)2=2n-1,
当n=1时,b1=1也适合此通项公式,所以bn=2n-1(n∈N*).
 由Tn=
由Tn=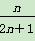 >
>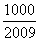 ,得n>
,得n>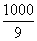 ,所以满足Tn>
,所以满足Tn>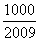 的最小正整数n为112.
的最小正整数n为112.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
下面是关于公差d>0的等差数列{an}的四个命题:
p1:数列{an}是递增数列;
p2:数列{nan}是递增数列;
p3:数列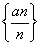 是递增数列;
是递增数列;
p4:数列{an+3nd}是递增数列.
其中的真命题为( )
A.p1,p2 B.p3,p4
C.p2,p3 D.p1,p4
查看答案和解析>>
科目:高中数学 来源: 题型:
已知等比数列{an}的所有项均为正数,首项a1=1,
且a4,3a3,a5成等差数列.
(1)求数列{an}的通项公式;
(2)数列{an+1-λan}的前n项和为Sn,若Sn=2n-1(n∈N*),求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的各项排成如图所示的三角形数阵,数阵中每一行的第一个数a1,a2,a4,a7,…构成等差数列{bn},Sn是{bn}的前n项和,且b1=a1=1,S5=15.
a1
a2 a3
a4 a5 a6
a7 a8 a9 a10
…
(1)若数阵中从第3行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知a9=16,求a50的值;
(2)设Tn=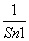 +
+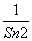 +…+
+…+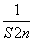 ,求Tn.
,求Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
若二次函数f(x)=4x2-2(p-2)x-2p2-p+1,在区间[-1,1]内至少存在一点c,使f(c)>0,则实数p的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com