
分析 (Ⅰ)由2a1=a0+a2,求得m=8,可得展开式的中间项是第五项,再根据通项公式求得结果.
(Ⅱ)在所给的等式中,分别令x=1、x=-1,可得2个等式,由这2个等式即可求得展开式中所有含x奇次幂的系数和.
解答 解:(Ⅰ)依题意a0=1,${a_1}=\frac{m}{2}$,${a_2}={C_m}^2{(\frac{1}{2})^2}$,由2a1=a0+a2
可得m=1(舍去),或m=8,
所以${(1+\frac{1}{2}x)^m}$展开式的中间项是第五项为:${T_5}=C_8^4{(\frac{1}{2}x)^4}=\frac{35}{8}{x^4}$;
(Ⅱ)${(1+\frac{1}{2}x)^m}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+…+{a_m}{x^m}$
即${(1+\frac{1}{2}x)^8}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+…+{a_8}{x^8}$
令x=1则${a_0}+{a_1}+{a_2}+{a_3}+…+{a_8}={(\frac{3}{2})^8}$,
令x=-1则${a_0}-{a_1}+{a_2}-{a_3}+…+{a_8}={(\frac{1}{2})^8}$,
所以${a_1}+{a_3}+{a_5}+{a_7}=\frac{{{3^8}-1}}{2^9}=\frac{205}{16}$,
所以展开式中含x的奇次幂的系数和为$\frac{205}{16}$.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式的系数和常用的方法是赋值法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份202x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数 y(十万) | 5 | 7 | 8 | 11 | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\stackrel{∧}{y}$=-10x-100 | B. | $\stackrel{∧}{y}$=10x-100 | C. | $\stackrel{∧}{y}$=-10x+200 | D. | $\stackrel{∧}{y}$=10x-200 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
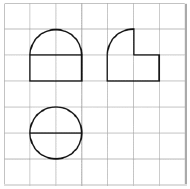
| A. | $\frac{7π}{2}$ | B. | 4π | C. | $\frac{9π}{2}$ | D. | 5π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com