
| A. | 24万元 | B. | 22万元 | C. | 18万元 | D. | 16万元 |
分析 根据条件建立不等式组即线性目标函数,利用图象可求该厂的日利润最大值.
解答 解:设甲、乙两种产品分别生产x、y件,工厂获得的利润为z又已知条件可得二元一次不等式组:
$\left\{\begin{array}{l}{x+2y≤8}\\{4x≤24}\\{4y≤16}\\{x≥0}\\{y≥0}\end{array}\right.$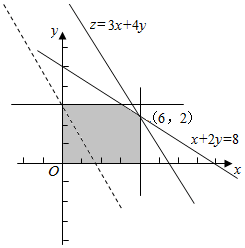
目标函数为z=3x+4y,
由 $\left\{\begin{array}{l}{x=6}\\{x+2y=8}\end{array}\right.$,可得 $\left\{\begin{array}{l}{x=6}\\{y=1}\end{array}\right.$,
利用线性规划可得x=6,y=1时,此时该厂的日利润最大为z=3×6+4=22万元,
故选:B.
点评 本题考查线性规划知识,考查利润最大,解题的关键是确定线性约束条件及线性目标函数.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
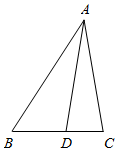 在△ABC中,角A,B,C的对应边分别为a,b,c,且三角形的面积为S=$\frac{{\sqrt{3}}}{2}$accosB.
在△ABC中,角A,B,C的对应边分别为a,b,c,且三角形的面积为S=$\frac{{\sqrt{3}}}{2}$accosB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a0.8>a0.7 | B. | 0.7a>0.6a | C. | loga0.7<loga0.8 | D. | 0.8lga>0.7lga |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
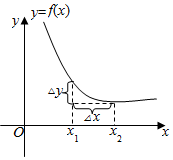 已知函数y=f(x)的图象如图,自变量x从x1变到x2,对应的函数y从f(x1)变到f(x2),设△x=x2-x1,确定各图的中△x,△y,$\frac{△y}{△x}$的正负.
已知函数y=f(x)的图象如图,自变量x从x1变到x2,对应的函数y从f(x1)变到f(x2),设△x=x2-x1,确定各图的中△x,△y,$\frac{△y}{△x}$的正负.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
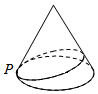 如图,一竖立在水平对面上的圆锥形物体的母线长为4m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为$4\sqrt{3}m$,则圆锥底面圆的半径等于( )
如图,一竖立在水平对面上的圆锥形物体的母线长为4m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为$4\sqrt{3}m$,则圆锥底面圆的半径等于( )| A. | 1m | B. | $\frac{3}{2}m$ | C. | $\frac{4}{3}m$ | D. | 2m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com