Question

3．AC是圆的直径，B、D在圆上且AB=$\sqrt{3}$，AD=$\sqrt{5}$，则$\overrightarrow{AC}$$•\overrightarrow{BD}$=2．

Answer 1

分析 可连接CD，CB，从而得到CD⊥AD，BC⊥AB，便可得到$\overrightarrow{AC}$在$\overrightarrow{AD}$方向上的投影就是AD，所以$\overrightarrow{AC}$$•\overrightarrow{BD}$=$\overrightarrow{AC}•\overrightarrow{AD}-\overrightarrow{AC}•\overrightarrow{AB}$=$\overrightarrow{|AC}||\overrightarrow{AD}|•COS∠CAD$-$|\overrightarrow{AC}||\overrightarrow{AB}|COS∠CAB$=AD²-AB²．

解答 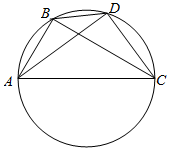解：如图，连接CD，CB；
∵AC为直径；
∴CD⊥AD，BC⊥AB；
∴$\overrightarrow{AC}$$•\overrightarrow{BD}$=$\overrightarrow{AC}•\overrightarrow{AD}-\overrightarrow{AC}•\overrightarrow{AB}$=$\overrightarrow{|AC}||\overrightarrow{AD}|•COS∠CAD$-$|\overrightarrow{AC}||\overrightarrow{AB}|COS∠CAB$=AD²-AB²=5-3=2；
故答案为：2．

点评 本题考查直径所对的圆周角为直角，余弦函数的定义，以及向量减法的几何意义，向量数量积的运算关键明确$\overrightarrow{AC}$在两个向量方向的投影；属于中档题．