

���� ��1����������õ�A�͵�C�����꣬�ٰ����Ǵ��������ߵķ������b��c��ֵ���ɵ������ߵĽ���ʽ��
��2����P��x0��0����x0��0�����������tan��OPC=$\frac{3}{{-x}_{0}}$���������������ļнǹ�ʽ���cos��$\overrightarrow{BC}$��$\overrightarrow{BD}$����ֵ���ɵ�tan��$\overrightarrow{BC}$��$\overrightarrow{BD}$����ֵ����ϡ�OPC=2��CBD���ö����ǵ����й�ʽ���x0��ֵ���ɵõ�P�����꣮
��3����Q��x1��${{x}_{1}}^{2}$-2x1-3����1��x1��3�����PQ��AC�ķ��̣������tan��PAF=$\frac{{k}_{FP}{-k}_{FA}}{1{+k}_{FP}{•k}_{FA}}$��ֵ���ɵ�F�����꣬�ٸ���F��ֱ��PQ�ϣ����Q������꣬�Ӷ��ó����ۣ�
���  �⣺��1����ͼ1����ֱ��AC�Ľ���ʽΪy=kx-3��
�⣺��1����ͼ1����ֱ��AC�Ľ���ʽΪy=kx-3��
��x=0����y=-3����C��0��-3����
�֡�tan��ACO=$\frac{1}{3}$����A��-1��0����
��$\left\{\begin{array}{l}{c=-3}\\{{��-1��}^{2}+b����-1��+c=0}\end{array}\right.$��
���b=-2��c=-3��
��������y=x2-2x-3��
��2����ͼ2���ߵ�P��x�Ḻ������һ���㣬
����P��x0��0����x0��0��
��C��0��-3����B��3��0����D��1��-4����
��Rt��POC��tan��OPC=$\frac{3}{{-x}_{0}}$=-$\frac{3}{{x}_{0}}$��
��$\overrightarrow{BC}$=��-3��-3����$\overrightarrow{BD}$=��-2��-4����
��cos��$\overrightarrow{BC}$��$\overrightarrow{BD}$��=$\frac{\overrightarrow{BC}•\overrightarrow{BD}}{|\overrightarrow{BC}|��|\overrightarrow{BD}|}$=$\frac{-3����-2��-3����-4��}{\sqrt{{��-3��}^{2}{+��-3��}^{2}}��\sqrt{{��-2��}^{2}{+��-4��}^{2}}}$=$\frac{3}{\sqrt{10}}$��
��cos��CBD=$\frac{3}{\sqrt{10}}$����sin��CBD=$\frac{1}{\sqrt{10}}$����tan��CBD=$\frac{1}{3}$��
�֡ߡ�OPC=2��CBD��tan2��CBD=$\frac{2tan��CBD}{1{-tan}^{2}��CBD}$=$\frac{2��\frac{1}{3}}{1{-��\frac{1}{3}��}^{2}}$=$\frac{3}{4}$��
��tan��CBD=$\frac{3}{4}$����-$\frac{3}{{x}_{0}}$=$\frac{3}{4}$�����x0=-4�����P������ΪP��-4��0����
��3����ͼ3��ʾ��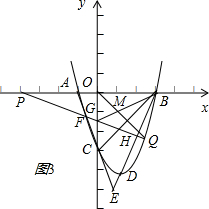
�ߵ�Q��������y=x2-2x-3�ϵ�һ���㣨��Q�ڵ����������ڶԳ����Ҳࣩ��
����Q��x1��${{x}_{1}}^{2}$-2x1-3����1��x1��3��
��ֱ��PQ�ķ���Ϊ$\frac{x+4}{{x}_{1}+4}$=$\frac{y}{{{x}_{1}}^{2}-2{x}_{1}-3}$�٣�ֱ��AC�ķ���Ϊy=-3x-3�ڣ�
�����F��t��-3t-3������kFA=-3��kFP=$\frac{3t+3}{-4-t}$��
��tan��PAF=$\frac{{k}_{FP}{-k}_{FA}}{1{+k}_{FP}{•k}_{FA}}$=$\frac{\frac{3t+3}{-4-t}+3}{1+\frac{3t+3}{-4-t}•��-3��}$=1��
���t=-$\frac{2}{5}$����F��-$\frac{2}{5}$��-$\frac{9}{5}$����
��F��ֱ��PQ�ϣ���$\frac{-\frac{2}{5}+4}{{x}_{1}+4}$=$\frac{-\frac{9}{5}}{{{x}_{1}}^{2}{-x}_{1}-3}$��
��2${{x}_{1}}^{2}$-x1-2=0�����x1=$\frac{1+\sqrt{17}}{4}$����x1=$\frac{1-\sqrt{17}}{4}$����ȥ����
��y1=${{��x}_{1}-1��}^{2}$-4=${��\frac{1+\sqrt{17}}{4}-1��}^{2}$-4=-$\frac{19+3\sqrt{17}}{8}$��
���Q��������$\frac{1+\sqrt{17}}{4}$��-$\frac{19+3\sqrt{17}}{8}$����
����P��-4��0����������ʽ���PQ�ķ���Ϊy=-$\frac{��19+\sqrt{37}��}{34+2\sqrt{17}}$x-$\frac{76+12\sqrt{17}}{34+2\sqrt{17}}$��
�ʵ�G������Ϊ��0��-$\frac{76+12\sqrt{17}}{34+2\sqrt{17}}$����
��ֱ��д��BG��OQ�ཻ����BG=$\sqrt{{3}^{2}{+��\frac{76+12\sqrt{17}}{34+2\sqrt{17}}��}^{2}}$��OQ=$\sqrt{{��\frac{1+\sqrt{17}}{4}��}^{2}{+��\frac{19+3\sqrt{17}}{8}��}^{2}}$��
���� ������Ҫ������κ�����ͼ������ʣ�ֱ�ߵ�б�ʹ�ʽ�������ǵ����й�ʽ��Ӧ�ã�������ת�������ν�ϵ���ѧ˼�룬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{3}{4}$] | B�� | [0��$\frac{3}{4}$] | C�� | [0��1�� | D�� | [0��1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com