
分析 (1)利用互斥事件的概率公式求解即可;
(2)由题意,X~B(5,$\frac{1}{3}$),求出相应的概率,即可求他扑出的点球个数X的分布列与期望.
解答 解:(1)当法国队胜一场,输2场时,P=C31×$\frac{1}{2}×\frac{1}{6}×\frac{1}{6}$=$\frac{1}{24}$;
当法国队打平3场时,P=$\frac{1}{3}×\frac{1}{3}×\frac{1}{3}$=$\frac{1}{27}$.
∴法国队积分为3分的概率=$\frac{1}{24}$+$\frac{1}{27}$=$\frac{17}{216}$;
(2)由题意,X~B(5,$\frac{1}{3}$),
P(X=0)=($\frac{2}{3}$)5=$\frac{32}{243}$,
P(X=1)=C51×$\frac{1}{3}$×($\frac{2}{3}$)4=$\frac{80}{243}$,
P(X=2)=C52×($\frac{1}{3}$)2×($\frac{2}{3}$)3=$\frac{80}{243}$,
P(X=3)=C53×($\frac{1}{3}$)3×($\frac{2}{3}$)2=$\frac{40}{243}$,
P(X=4)=C54×($\frac{1}{3}$)4×($\frac{2}{3}$)=$\frac{10}{243}$,
P(X=5)=C55×($\frac{1}{3}$)5=$\frac{1}{243}$,
X的分布列为
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{32}{243}$ | $\frac{80}{243}$ | $\frac{80}{243}$ | $\frac{40}{243}$ | $\frac{10}{243}$ | $\frac{1}{243}$ |
点评 本题考查离散型随机变量的分布列,期望的求法,互斥事件概率公式的应用,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
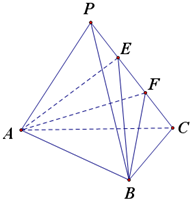 在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.
在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com