
分析 根据奇函数的性质求得a、b的值,可得a+b的值.由条件利用分段函数,解三角不等式,求得x的范围.
解答 解:由奇函数f(x)=$\left\{\begin{array}{l}{acosx-\sqrt{3}sinx+c,x≥0}\\{cosx+bsinx-c,x<0}\end{array}\right.$,不妨设x>0,则-x<0,
由f(-x)=-f(x),可得 cos(-x)-bsinx-c=-[acosx-$\sqrt{3}$sinx+c],
可得a=-1,b=-$\sqrt{3}$.
再根据f(0)=a-0+c=-1+c=0,可得c=1,故a+b=-1-$\sqrt{3}$.
由f(x)>f(-x)=-f(x),可得2f(x)>0.
根据f(x)=$\left\{\begin{array}{l}{-cosx-\sqrt{3}sinx+1,x≥0}\\{cosx-\sqrt{3}sinx-1,x<0}\end{array}\right.$,可得$\left\{\begin{array}{l}{x≥0}\\{-cosx-\sqrt{3}sinx+1>0}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{x<0}\\{cosx-\sqrt{3}sinx-1>0}\end{array}\right.$②.
再根据x∈[-π,π],且x≥0,可得x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
再由①可得sin(x+$\frac{π}{6}$)<$\frac{1}{2}$,求得$\frac{5π}{6}$<x+$\frac{π}{6}$≤$\frac{7π}{6}$,即 $\frac{2π}{3}$<x≤π.
再根据x∈[-π,π],且x<0,可得x+$\frac{π}{3}$∈[-$\frac{2π}{3}$,$\frac{π}{3}$),
由②可得cos(x+$\frac{π}{3}$)>$\frac{1}{2}$,求得-$\frac{π}{3}$<x+$\frac{π}{3}$<$\frac{π}{3}$,即-$\frac{2π}{3}$<x<0.
综上可得,不等式f(x)>f(-x)在x∈[-π,π]上的解集为($\frac{2π}{3}$,π]∪(-$\frac{2π}{3}$,0),
故答案为:-1-$\sqrt{3}$;($\frac{2π}{3}$,π]∪(-$\frac{2π}{3}$,0).
点评 本题主要考查奇函数的性质,分段函数的应用,解三角不等式,属于中档题.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:填空题
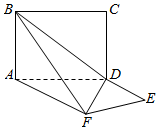 平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.
平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
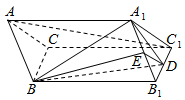 如图,在三棱柱ABC-A1B1C1中,A1B1=A1C1,点D,E分别是B1C1,A1B1的中点,AA1=AB=BD=1,∠A1AB=60°.
如图,在三棱柱ABC-A1B1C1中,A1B1=A1C1,点D,E分别是B1C1,A1B1的中点,AA1=AB=BD=1,∠A1AB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6斤 | B. | 9斤 | C. | 9.5斤 | D. | 12斤 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com