Question

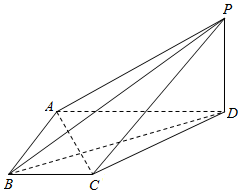
11．四棱锥P-ABCD中，PD⊥底面ABCD，AD∥BC，AC⊥DB，∠CAD=60°，AD=2，PD=1．
（Ⅰ）证明：AC⊥BP；
（Ⅱ）求二面角C-AP-D的平面角的余弦值．

Answer 1

分析 （Ⅰ）根据线面垂直的性质即可得到AC⊥PD，而由条件AC⊥BD，这样根据线面垂直的判定定理便可得出AC⊥平面PBD，进而便可证出AC⊥BP；
（Ⅱ）可设AC与BD交于点O，这样由条件便可分别以OD，OA为x轴，y轴，建立空间直角坐标系，从而可以求出点O，D，A，P四点的坐标，进而得出向量$\overrightarrow{OA}，\overrightarrow{OP}，\overrightarrow{AD}，\overrightarrow{DP}$的坐标，可设平面ACP的法向量$\overrightarrow{m}=（{x}_{1}，{y}_{1}，{z}_{1}）$，平面ADP的法向量$\overrightarrow{n}=（{x}_{2}，{y}_{2}，{z}_{2}）$，这样根据$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{OA}=0}\\{\overrightarrow{m}•\overrightarrow{OP}=0}\end{array}\right.$便可得出法向量$\overrightarrow{m}$的坐标，同理便可得出法向量$\overrightarrow{n}$的坐标，从而便可求出$cos＜\overrightarrow{m}，\overrightarrow{n}＞$的值，即得出二面角C-AP-D的平面角的余弦值．

解答 解：（Ⅰ）证明：∵PD⊥底面ABCD，AC?平面ABCD；
∴AC⊥PD；
又AC⊥BD，BD∩PD=D；
∴AC⊥平面PBD，BP?平面PBD；
∴AC⊥BP；
（Ⅱ）设AC∩BD=O，以O为坐标原点，OD，OA为x，y轴建立如图空间直角坐标系O-xyz，则：O（0，0，0），D（$\sqrt{3}$，0，0），A（0，1，0），P（$\sqrt{3}$，0，1）；
∴$\overrightarrow{OA}=（0，1，0），\overrightarrow{OP}=（\sqrt{3}，0，1）$，$\overrightarrow{AD}=（\sqrt{3}，-1，0）$，$\overrightarrow{DP}=（0，0，1）$；
设平面ACP的法向量$\overrightarrow{m}=（{x}_{1}，{y}_{1}，{z}_{1}）$，平面ADP的法向量$\overrightarrow{n}=（{x}_{2}，{y}_{2}，{z}_{2}）$；
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{OA}=0}\\{\overrightarrow{m}•\overrightarrow{OP}=0}\end{array}\right.$得，$\left\{\begin{array}{l}{{y}_{1}=0}\\{\sqrt{3}{x}_{1}+{z}_{1}=0}\end{array}\right.$，取x₁=1，则$\overrightarrow{m}=（1，0，-\sqrt{3}）$；
同理，由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AD}=0}\\{\overrightarrow{n}•\overrightarrow{DP}=0}\end{array}\right.$得，$\overrightarrow{n}=（1，\sqrt{3}，0）$；
∴$cos＜\overrightarrow{m}，\overrightarrow{n}＞=\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{1}{2×2}=\frac{1}{4}$；
∴二面角C-AP-D的平面角的余弦值为$\frac{1}{4}$．

点评 考查线面垂直的性质，线面垂直的判定定理，以及通过建立空间直角坐标系，利用向量的坐标解决二面角的平面角问题的方法，能求空间点的坐标，根据点的坐标可求向量的坐标，以及平面法向量的概念及求法，清楚两平面法向量的夹角和两平面所成平面角大小的关系，向量夹角余弦的坐标公式．