
分析 (I)利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性,得出结论.
(II)由条件求得sin(2α+$\frac{π}{6}$)的值以及2α+$\frac{π}{6}$的范围,可得cos(2α+$\frac{π}{6}$)的值,再根据sin2α=sin(2α+$\frac{π}{6}$-$\frac{π}{6}$),利用两角差的正弦公式,求得sin2α的值.
解答 解:(I)∵函数f(x)=$\sqrt{3}$sinxcosx+cos2x=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1+cos2x}{2}$=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$,
∴函数f(x)的最小正周期为$\frac{2π}{2}$=π.
(II)若-$\frac{π}{2}$<α<0,则2α+$\frac{π}{6}$∈(-$\frac{5π}{6}$,$\frac{π}{6}$),
∴f(α)=sin(2α+$\frac{π}{6}$)+$\frac{1}{2}$=$\frac{5}{6}$,∴sin(2α+$\frac{π}{6}$)=$\frac{1}{3}$,∴2α+$\frac{π}{6}$∈(0,$\frac{π}{6}$),
∴cos(2α+$\frac{π}{6}$)=$\sqrt{{1-sin}^{2}(2α+\frac{π}{6})}$=$\frac{2\sqrt{2}}{3}$,
∴sin2α=sin(2α+$\frac{π}{6}$-$\frac{π}{6}$)=sin(2α+$\frac{π}{6}$)cos$\frac{π}{6}$-cos(2α+$\frac{π}{6}$)sin$\frac{π}{6}$=$\frac{1}{3}•\frac{\sqrt{3}}{2}$-$\frac{2\sqrt{2}}{3}•\frac{1}{2}$=$\frac{\sqrt{3}-2\sqrt{2}}{6}$.
点评 本题主要考查三角恒等变换,正弦函数的周期性,同角三角函数的基本关系,两角差的三角公式的应用,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
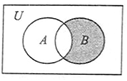
| A. | {-1,2} | B. | {-1,0} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
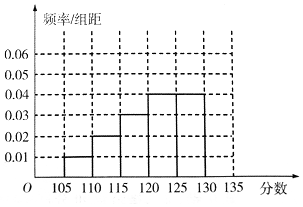 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:| 组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
| 第一组 | [105,110) | 15 | 0.3 |
| 第二组 | [110,115) | 30 | 0.3 |
| 第三组 | [115,120) | x | 0.4 |
| 第四组 | [120,125) | 100 | 0.5 |
| 第五组 | [125,130) | 120 | 0.6 |
| 第六组 | [130,135) | 195 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{5}$,1] | B. | [1,5] | C. | [$\frac{1}{5}$,5] | D. | (-∞,$\frac{1}{5}$]∪[5,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com