
分析 (1)运用分段函数的各段的解析式,计算即可得到;
(2)对a讨论,由各段的解析式,解方程可得a的值.
解答 解:(1)f(-2)=-2+2=0;
f(-$\frac{3}{2}$)=-$\frac{3}{2}$+2=$\frac{1}{2}$,
f(f(-$\frac{3}{2}$))=f($\frac{1}{2}$)=2×$\frac{1}{2}$=1;
(2)若a≤-1,则a+2=3,解得a=1,舍去;
若-1<a<2时,则2a=3,解得a=$\frac{3}{2}$,成立;
若a≥2时,则$\frac{{a}^{2}}{2}$=3,解得a=$\sqrt{6}$,成立.
综上可得a=$\frac{3}{2}$或a=$\sqrt{6}$.
点评 本题考查分段函数的运用:求自变量的值和函数值,考查运算能力,属于基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | x1 | $\frac{1}{3}$ | x2 | $\frac{7}{3}$ | x3 |
| Asin(ωx+ϕ)+B | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
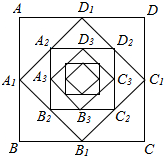 如图,正方形ABCD的边长为1,联结这个正方形各边的中点得到一个小正方形A1B1C1D1;又联结这个小正方形各边的中点得到一个更小的正方形A2B2C2D2;如此无限继续下去,设各正方形的边长依大小顺序构成数列{an}.
如图,正方形ABCD的边长为1,联结这个正方形各边的中点得到一个小正方形A1B1C1D1;又联结这个小正方形各边的中点得到一个更小的正方形A2B2C2D2;如此无限继续下去,设各正方形的边长依大小顺序构成数列{an}.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com