
| A. | 5$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{10}$ | D. | $\sqrt{10}$ |
分析 求出sinA,sinB,利用两角和的余弦公式计算cosC,根据内心的性质得出a$\overrightarrow{OA}$+b$\sqrt{10}$$\overrightarrow{OB}$+c$\overrightarrow{OC}$=$\overrightarrow{0}$,令a=2$\sqrt{5}$,b=$\sqrt{10}$,则用余弦定理计算c即为m的值.
解答 解:∵cosA=$\frac{2\sqrt{5}}{5}$,cosB=$\frac{3\sqrt{10}}{10}$,∴sinA=$\frac{\sqrt{5}}{5}$,sinB=$\frac{\sqrt{10}}{10}$.
∴cosC=-cos(A+B)=sinAsinB-cosAcosB=-$\frac{\sqrt{2}}{2}$.
不妨设a=2$\sqrt{5}$,b=$\sqrt{10}$,则c2=$\sqrt{{a}^{2}+{b}^{2}-2abcosC}$=5$\sqrt{2}$.
∵O为△ABC内心,∴a$\overrightarrow{OA}$+b$\sqrt{10}$$\overrightarrow{OB}$+c$\overrightarrow{OC}$=$\overrightarrow{0}$,即2$\sqrt{5}$$\overrightarrow{OA}$+$\sqrt{10}$$\overrightarrow{OB}$+c$\overrightarrow{OC}$=$\overrightarrow{0}$.
∴m=c=5$\sqrt{2}$.
故选A.
点评 本题考查了三角形内心的性质,余弦定理,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{6}$ | B. | x=$\frac{11π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈R使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0” | |
| B. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”,则¬p是真命题 | |
| C. | “p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | |
| D. | “a<1”是“${log_{\frac{1}{2}}}$a>0”的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
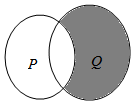 已知集合P={x|y=$\frac{1}{\sqrt{4-x}}$},Q={y|y=log2(x2+4)},集合P与集合Q所对应的韦恩图如图所示,则图中阴影部分表示的集合是( )
已知集合P={x|y=$\frac{1}{\sqrt{4-x}}$},Q={y|y=log2(x2+4)},集合P与集合Q所对应的韦恩图如图所示,则图中阴影部分表示的集合是( )| A. | {x|2≤x<4} | B. | {x|x<2} | C. | {x|x≥4} | D. | {x|x<2,或x≥4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com