
ЁОЬтФПЁПФГЭјЙКЦНЬЈЮЊСЫНтФГЪаОгУёдкИУЦНЬЈЕФЯћЗбЧщПіЃЌДгИУЪаЪЙгУЦфЦНЬЈЧвУПжмЦНОљЯћЗбЖюГЌЙ§100дЊЕФШЫдБжаЫцЛњГщШЁСЫ100УћЃЌВЂЛцжЦгвЭМЫљЪОЦЕТЪЗжВМжБЗНЭМЃЌвбжЊжЎМфШ§зщЕФШЫЪ§ПЩЙЙГЩЕШВюЪ§Са.

ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЗжЮіШЫдБЖд100УћЕїВщЖдЯѓЕФадБ№НјааЭГМЦЗЂЯжЃЌЯћЗбН№ЖюВЛЕЭгк300дЊЕФФаадга20ШЫЃЌЕЭгк300дЊЕФФаадга25ШЫЃЌИљОнЭГМЦЪ§ОнЭъГЩЯТСа![]() СаСЊБэЃЌВЂХаЖЯЪЧЗёга
СаСЊБэЃЌВЂХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊЯћЗбН№ЖюгыадБ№гаЙиЃП
ЕФАбЮеШЯЮЊЯћЗбН№ЖюгыадБ№гаЙиЃП
ЃЈ3ЃЉЗжЮіШЫдБЖдГщШЁЖдЯѓУПжмЕФЯћЗбН№Жю![]() гыФъСф
гыФъСф![]() НјвЛВНЗжЮіЃЌЗЂЯжЫћУЧЯпадЯрЙиЃЌЕУЕНЛиЙщЗНГЬ
НјвЛВНЗжЮіЃЌЗЂЯжЫћУЧЯпадЯрЙиЃЌЕУЕНЛиЙщЗНГЬ![]() .вбжЊ100УћЪЙгУепЕФЦНОљФъСфЮЊ38ЫъЃЌЪдХаЖЯвЛУћФъСфЮЊ25ЫъЕФФъЧсШЫУПжмЕФЦНОљЯћЗбН№ЖюЮЊЖрЩй.ЃЈЭЌвЛзщЪ§ОнгУИУЧјМфЕФжаЕужЕДњЬцЃЉ
.вбжЊ100УћЪЙгУепЕФЦНОљФъСфЮЊ38ЫъЃЌЪдХаЖЯвЛУћФъСфЮЊ25ЫъЕФФъЧсШЫУПжмЕФЦНОљЯћЗбН№ЖюЮЊЖрЩй.ЃЈЭЌвЛзщЪ§ОнгУИУЧјМфЕФжаЕужЕДњЬцЃЉ

![]() ЃЌЦфжа
ЃЌЦфжа![]()
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉга
ЃЈ2ЃЉга![]() ЕФАбЮеЃЈ3ЃЉ395
ЕФАбЮеЃЈ3ЃЉ395
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнвбжЊСаЙигкm,nЕФЗНГЬзщНтжЎМДЕУ.(2)ЯШЭъГЩ2ЁС2СаСЊБэЃЌдйМЦЫу![]() ЕФжЕХаЖЯ.(3)ЯШЧѓЕїВщЖдЯѓЕФжмЦНОљЯћЗбЃЌдйЧѓbЕФжЕ.
ЕФжЕХаЖЯ.(3)ЯШЧѓЕїВщЖдЯѓЕФжмЦНОљЯћЗбЃЌдйЧѓbЕФжЕ.
ЯъНтЃКЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМПЩжЊЃЌ![]() ЃЌ
ЃЌ
гЩжаМфШ§зщЕФШЫЪ§ГЩЕШВюЪ§СаПЩжЊ![]() ЃЌ
ЃЌ
ПЩНтЕУ![]()
ЃЈ2ЃЉжмЦНОљЯћЗбВЛЕЭгк300дЊЕФЦЕТЪЮЊ![]() ЃЌ
ЃЌ
вђДЫ100ШЫжаЃЌжмЦНОљЯћЗбВЛЕЭгк300дЊЕФШЫЪ§ЮЊ![]() ШЫ.
ШЫ.
Ыљвд![]() СаСЊБэЮЊ
СаСЊБэЮЊ
Фаад | ХЎад | КЯМЦ | |
ЯћЗбН№ЖюЁн300 | 20 | 40 | 60 |
ЯћЗбН№ЖюЃМ300 | 25 | 15 | 40 |
КЯМЦ | 45 | 55 | 100 |
![]()
Ыљвдга![]() ЕФАбЮеШЯЮЊЯћЗбН№ЖюгыадБ№гаЙи.
ЕФАбЮеШЯЮЊЯћЗбН№ЖюгыадБ№гаЙи.
ЃЈ3ЃЉЕїВщЖдЯѓЕФжмЦНОљЯћЗбЮЊ
![]() ЃЌ
ЃЌ
гЩЬтвт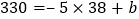 ЃЌЁр
ЃЌЁр![]()
![]() .
.


 ПЮПЮСЗНЫеЯЕСаД№АИ
ПЮПЮСЗНЫеЯЕСаД№АИ УћХЦжабЇПЮЪБзївЕЯЕСаД№АИ
УћХЦжабЇПЮЪБзївЕЯЕСаД№АИ УїЬьНЬг§ПЮЪБЬибЕЯЕСаД№АИ
УїЬьНЬг§ПЮЪБЬибЕЯЕСаД№АИ еуНаТПЮГЬШ§ЮЌФПБъВтЦРПЮЪБЬибЕЯЕСаД№АИ
еуНаТПЮГЬШ§ЮЌФПБъВтЦРПЮЪБЬибЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭММзжаЕФСНЬѕЧњЯпЗжБ№БэЪОФГРэЯызДЬЌЯТВЖЪГепКЭБЛВЖЪГепЪ§СПЫцЪБМфЕФБфЛЏЙцТЩЁЂЖдВЖЪГепКЭБЛВЖЪГепЪ§СПжЎМфЕФЙиЯЕУшЪіДэЮѓЕФЪЧЃЈ ЃЉ
A. ВЖЪГепКЭБЛВЖЪГепЪ§СПгыЪБМфвд![]() ФъЮЊжмЦк
ФъЮЊжмЦк
B. гЩЭМПЩжЊЃЌЕБВЖЪГепЪ§СПдіЖрЕФЙ§ГЬжаЃЌБЛВЖЪГепЪ§СПЯШдіЖрКѓМѕЩй
C. ВЖЪГепКЭБЛВЖЪГепЪ§СПжЎМфЕФЙиЯЕПЩвдгУЭМ1ввУшЪі
D. ВЖЪГепЕФЪ§СПдкЕк![]() ФъКЭ
ФъКЭ![]() ФъжЎМфЪ§СПдкМБЫйМѕЩй
ФъжЎМфЪ§СПдкМБЫйМѕЩй
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
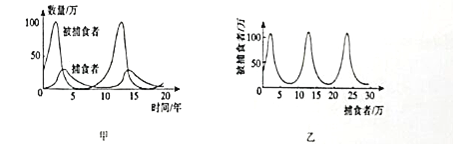
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвддЕуOЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌСНжжзјБъЯЕжаШЁЯрЭЌЕФГЄЖШЕЅЮЛ.вбжЊжБЯпlЕФВЮЪ§ЗНГЬЮЊ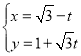 ЃЈtЮЊВЮЪ§ЃЉЃЌЧњЯпCЕФМЋзјБъЗНГЬЮЊІбЃН4sinЃЈІШ+
ЃЈtЮЊВЮЪ§ЃЉЃЌЧњЯпCЕФМЋзјБъЗНГЬЮЊІбЃН4sinЃЈІШ+![]() ЃЉ.
ЃЉ.
ЃЈ1ЃЉЧѓжБЯпlЕФЦеЭЈЗНГЬгыЧњЯпCЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯпlгыЧњЯпCНЛгкMЃЌNСНЕуЃЌЧѓЁїMONЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗжаЁАжёОХНкЁБЮЪЬтЃКЯжгавЛИљ9НкЕФжёзгЃЌздЩЯЖјЯТИїНкЕФШнЛ§ГЩЕШВюЪ§СаЃЌЩЯУц4НкЕФШнЛ§ЙВ3Щ§ЃЌЯТУц3НкЕФШнЛ§ЙВ4Щ§ЃЌдђЕк6НкЕФШнЛ§ЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫМрПиФГжжСуМўЕФвЛЬѕЩњВњЯпЕФЩњВњЙ§ГЬЃЌМьбщдБУПЬьДгИУЩњВњЯпЩЯЫцЛњГщШЁ16ИіСуМўЃЌВЂВтСПЦфГпДчЃЈЕЅЮЛЃКcmЃЉЃЎИљОнГЄЦкЩњВњОбщЃЌПЩвдШЯЮЊетЬѕЩњВњЯпе§ГЃзДЬЌЯТЩњВњЕФСуМўЕФГпДчЗўДге§ЬЌЗжВМNЃЈІЬЃЌІв2ЃЉЃЎ
ЃЈ1ЃЉМйЩшЩњВњзДЬЌе§ГЃЃЌМЧXБэЪОвЛЬьФкГщШЁЕФ16ИіСуМўжаЦфГпДчдкЃЈІЬ-3ІвЃЌІЬ+3ІвЃЉжЎЭтЕФСуМўЪ§ЃЌЧѓPЃЈXЁн1ЃЉМАXЕФЪ§бЇЦкЭћЃЛ
ЃЈ2ЃЉвЛЬьФкГщМьСуМўжаЃЌШчЙћГіЯжСЫГпДчдкЃЈІЬ-3ІвЃЌІЬ+3ІвЃЉжЎЭтЕФСуМўЃЌОЭШЯЮЊетЬѕЩњВњЯпдкетвЛЬьЕФЩњВњЙ§ГЬПЩФмГіЯжСЫвьГЃЧщПіЃЌашЖдЕБЬьЕФЩњВњЙ§ГЬНјааМьВщЃЌЪдгУЫљбЇжЊЪЖЫЕУїЩЯЪіМрПиЩњВњЙ§ГЬЗНЗЈЕФКЯРэадЃЛ
ИНЃКШєЫцЛњБфСПZЗўДге§ЬЌЗжВМNЃЈІЬЃЌ![]() ЃЉЃЌдђPЃЈІЬ-3ІвЃМZЃМІЬ+3ІвЃЉ=0.9974ЃЌ
ЃЉЃЌдђPЃЈІЬ-3ІвЃМZЃМІЬ+3ІвЃЉ=0.9974ЃЌ![]() ЃЌЃЎ
ЃЌЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаГізтГЕЪеЗбБъзМШчЯТЃКЦ№ВНМлЮЊ8дЊЃЌЦ№ВНРяГЬЮЊ3kmЃЈВЛГЌЙ§3kmАДЦ№ВНМлИЖЗбЃЉЃЛГЌЙ§3kmЕЋВЛГЌЙ§8kmЪБЃЌГЌЙ§ВПЗжАДУПЧЇУз2.15дЊЪеЗбЃКГЌЙ§8kmЪБЃЌГЌЙ§ВПЗжАДУПЧЇУз2.85дЊЪеЗбЃЌСэУПДЮГЫзјашИЖШМгЭИНМгЗб1дЊЃЎЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
A.ГізтГЕааЪЛ2kmЃЌГЫПЭашИЖЗб8дЊ
B.ГізтГЕааЪЛ4kmЃЌГЫПЭашИЖЗб9.6дЊ
C.ГізтГЕааЪЛ10kmЃЌГЫПЭашИЖЗб25.45дЊ
D.ФГШЫГЫГізтГЕааЪЛ5kmСНДЮЕФЗбгУГЌЙ§ЫћГЫГізтГЕааЪЛ10kmвЛДЮЕФЗбгУ
E.ФГШЫГЫзјвЛДЮГізтГЕИЖЗб22.6дЊЃЌдђДЫДЮГізтГЕааЪЛСЫ9km
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаХЯЂПЦММЕФНјВНКЭЛЅСЊЭјЩЬвЕФЃЪНЕФаЫЦ№ЃЌШЋЗНЮЛЕиИФБфСЫДѓМвН№ШкЯћЗбЕФЯАЙпКЭН№ШкНЛвзФЃЪНЃЌЯждквјааЕФДѓВПЗжвЕЮёЖМПЩвдЭЈЙ§жЧФмжеЖЫЩшБИЭъГЩЃЌЖрМввјаажАдБШЫЪ§дкЧФШЛМѕЩй.ФГвјааЯжгажАдБ320ШЫЃЌЦНОљУПШЫУПФъПЩДДРћ20ЭђдЊ.ОнЦРЙРЃЌдкОгЊЬѕМўВЛБфЕФЧАЬсЯТЃЌУПВУдБ1ШЫЃЌдђСєИкжАдБУПШЫУПФъЖрДДРћ0.2ЭђдЊЃЌЕЋвјааашИЖЯТИкжАдБУПШЫУПФъ6ЭђдЊЕФЩњЛюЗбЃЌВЂЧвИУвјаае§ГЃдЫзЊЫљашШЫЪ§ВЛЕУаЁгкЯжгажАдБЕФ![]() ЃЌЮЊЪЙВУдБКѓЛёЕУЕФОМУаЇвцзюДѓЃЌИУвјаагІВУдБЖрЩйШЫЃПДЫЪБвјааЫљЛёЕУЕФзюДѓОМУаЇвцЪЧЖрЩйЭђдЊЃП
ЃЌЮЊЪЙВУдБКѓЛёЕУЕФОМУаЇвцзюДѓЃЌИУвјаагІВУдБЖрЩйШЫЃПДЫЪБвјааЫљЛёЕУЕФзюДѓОМУаЇвцЪЧЖрЩйЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌ
ЃЌ![]() ЕФЫФИіЖЅЕуЮЇГЩЕФЫФБпаЮЕФУцЛ§ЮЊ
ЕФЫФИіЖЅЕуЮЇГЩЕФЫФБпаЮЕФУцЛ§ЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§![]() ЕФзѓНЙЕу
ЕФзѓНЙЕу![]() зїжБЯп
зїжБЯп![]() гы
гы![]() НЛгк
НЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЯпЖЮ
СНЕуЃЌЯпЖЮ![]() ЕФжаЕуЮЊ
ЕФжаЕуЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃЈ
ЃЈ![]() ЮЊзјБъдЕуЃЉгыжБЯп
ЮЊзјБъдЕуЃЉгыжБЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЪЧЗёДцдкжБЯп
ЃЌЪЧЗёДцдкжБЯп![]() ЪЙЕУ
ЪЙЕУ![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌШєДцдкЃЌЧѓГі
ЮЊЕШбќжБНЧШ§НЧаЮЃЌШєДцдкЃЌЧѓГі![]() ЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНxexЉax2ЉxЃЛ
ЃЈ1ЃЉШєfЃЈxЃЉдкxЃНЉ1ДІШЁЕУМЋжЕЃЌЧѓaЕФжЕМАfЃЈxЃЉЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉЕБxЃО1ЪБЃЌfЃЈxЃЉЃО0КуГЩСЂЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com