
已知命题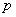 :“函数
:“函数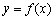 的图像关于点
的图像关于点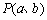 成中心对称图形”的充要条件为“函数
成中心对称图形”的充要条件为“函数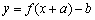 是奇函数”.
是奇函数”.
(1)试判断命题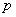 的真假?并说明理由;
的真假?并说明理由;
(2)设函数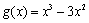 ,求函数
,求函数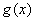 图像对称中心的坐标;
图像对称中心的坐标;
(3)试判断“存在实数a和b,使得函数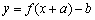 是偶函数”是“函数
是偶函数”是“函数 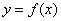 的图像关于某直线成轴对称图像”成立的什么条件?请说明理由.
的图像关于某直线成轴对称图像”成立的什么条件?请说明理由.
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com