
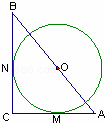
如图,在Rt△ABC中,∠C=90°,⊙O分别切AC、BC于M、N,圆心O在AB上,⊙O的半径为4,OA=5,则OB的长为 _________ .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
设F1,F2分别为双曲线C: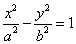 (a>0,b>0)的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线某条渐近线于M、N两点,且满足
(a>0,b>0)的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线某条渐近线于M、N两点,且满足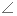 MAN=120o,则该双曲线的离心率为 ( )
MAN=120o,则该双曲线的离心率为 ( )
A. 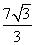 B.
B. 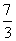 C.
C. 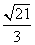 D.
D.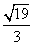
查看答案和解析>>
科目:高中数学 来源: 题型:
设某中学高三的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为y=0.85x﹣85.71,则下列结论中不正确的是( )
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心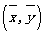
C. 若该中学高三某女生身高增加1cm,则其体重约增加0.85kg
D. 若该中学高三某女生身高为170cm,则可断定其体重必为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
某校举行中学生“日常生活小常识”知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题者则被淘汰.已知选手甲答对每个题的概率均为 ,且相互间没有影响.
,且相互间没有影响.
(1) 求选手甲进入复赛的概率;
(2) 设选手甲在初赛中答题的个数为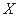 ,试求
,试求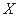 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题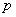 :“函数
:“函数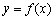 的图像关于点
的图像关于点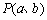 成中心对称图形”的充要条件为“函数
成中心对称图形”的充要条件为“函数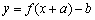 是奇函数”.
是奇函数”.
(1)试判断命题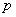 的真假?并说明理由;
的真假?并说明理由;
(2)设函数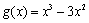 ,求函数
,求函数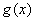 图像对称中心的坐标;
图像对称中心的坐标;
(3)试判断“存在实数a和b,使得函数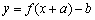 是偶函数”是“函数
是偶函数”是“函数 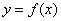 的图像关于某直线成轴对称图像”成立的什么条件?请说明理由.
的图像关于某直线成轴对称图像”成立的什么条件?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com