
 如图,在平面四边形ABCD中,若AB=1,BC=$\sqrt{2}$,AD=$\sqrt{2}$DC,∠ACD=90°,则对角线BD的最大值为3.
如图,在平面四边形ABCD中,若AB=1,BC=$\sqrt{2}$,AD=$\sqrt{2}$DC,∠ACD=90°,则对角线BD的最大值为3. 分析 设∠ABC=α,∠ACB=β,则在△ABC中,由余弦定理得AC2=3-2$\sqrt{2}$cosα.
由正弦定理得$\frac{AB}{sinβ}=\frac{AC}{sinα}$,即sinβ=$\frac{sinα}{AC}$
在△BCD中,可得BD2=BC2+CD2-2BC•CD•cos(900+β)=2+3-2$\sqrt{2}$cosα+2×$\sqrt{2}$×AC×$\frac{sinα}{AC}$=5+2$\sqrt{2}(sinα-cosα)$=5+4sin($α-\frac{π}{4}$)即可求解.
解答 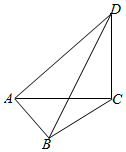 解:设∠ABC=α,∠ACB=β,则在△ABC中,由余弦定理得AC2=3-2$\sqrt{2}$cosα.
解:设∠ABC=α,∠ACB=β,则在△ABC中,由余弦定理得AC2=3-2$\sqrt{2}$cosα.
由正弦定理得$\frac{AB}{sinβ}=\frac{AC}{sinα}$,即sinβ=$\frac{sinα}{AC}$
∵AD=$\sqrt{2}$DC,∠ACD=90°,∴AC=CD
在△BCD中,由余弦定理得:BD2=BC2+CD2-2BC•CD•cos(900+β)
即DB2=2+3-2$\sqrt{2}$cosα+2×$\sqrt{2}$×AC×$\frac{sinα}{AC}$=5+2$\sqrt{2}(sinα-cosα)$
=5+4sin($α-\frac{π}{4}$)
∴当α=$\frac{3π}{4}$时,对角线BD最大,最大值为3,
故答案为:3
点评 本题考查了正余弦定理的应用,考查了转化思想、函数思想,属于难题.


科目:高中数学 来源: 题型:填空题
 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中m,n的比值$\frac{m}{n}$=$\frac{3}{8}$.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中m,n的比值$\frac{m}{n}$=$\frac{3}{8}$.查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三10月月考数学(文)试卷(解析版) 题型:选择题
(改编)已知复数 ,则复数
,则复数 在复平面上对应的点位于( )
在复平面上对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:解答题
某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
年龄(岁) | 频率 | |
第1组 |
| 0.1 |
第2组 |
| 0.1 |
第3组 |
| 0.4 |
第4组 |
| 0.3 |
第5组 |
| 0.1 |
(1)应分别在第1,2,3组中抽取志愿者多少人?
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知正方形ABCD与矩形ACEF所在的平面互相垂直,AB=2,AF=1.
如图,已知正方形ABCD与矩形ACEF所在的平面互相垂直,AB=2,AF=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是正方体的平面展开图,在这个正方体中,
如图是正方体的平面展开图,在这个正方体中,| A. | ③ | B. | ③④ | C. | ①③ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com