
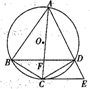
 如图,ABCD是圆O的内接四边形,点C是$\widehat{BD}$的中点,切线CE交AD的延长线于E,AC交BD于F.
如图,ABCD是圆O的内接四边形,点C是$\widehat{BD}$的中点,切线CE交AD的延长线于E,AC交BD于F.分析 (Ⅰ)如图,连接OC,证明△AFD∽△CDE,即可证明:∠AFD=∠CDE;
(Ⅱ)比值与$\frac{AE}{CE}$相等的线段共有7组,只需任写出其中5组即可.
解答 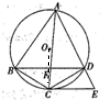 (Ⅰ)证明:如图,连接OC,
(Ⅰ)证明:如图,连接OC,
因为C是$\widehat{BD}$的中点,所以OC⊥BD.
因为CE为圆O的切线,所以OC⊥CE,
所以BD∥CE,所以∠E=∠FDA.
又因为∠DAF=∠DCE,
所以△AFD∽△CDE,
所以∠AFD=∠CDE…(5分)
(Ⅱ)解:比值与$\frac{AE}{CE}$相等的线段共有7组,只需任写出其中5组即可,$\frac{CE}{DE},\frac{AD}{FD},\frac{AB}{BF},\frac{BC}{CF},\frac{DC}{CF}$.…(10分)
点评 本题考查圆的弦切角定理和三角形相似的判定定理和性质定理的运用,考查推理和运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
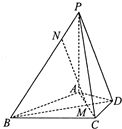 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
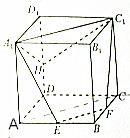 如图,在正方体ABCD-A1B1C1D1中,棱长是1,E、F分别是AB、BC的中点,H是DD1上任意一点.
如图,在正方体ABCD-A1B1C1D1中,棱长是1,E、F分别是AB、BC的中点,H是DD1上任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com