
分析 由题意可得,f(2013)=f(2012)-f(2011)=f(2011)-f(2010)-f(2011)=-f(2010),逐步代入可得f(2013)=f(2007),结合此规律可把所求的式子转化为f(0),即可求解.
解答 解:由题意可得,f(2013)=f(2012)-f(2011)=f(2011)-f(2010)-f(2011)=-f(2010)
而f(2010)=f(2009)-f(2008)=f(2008)-f(2007)-f(2008)=-f(2007)
∴f(2013)=f(2007)=f(2001)=…=f(3)=f(2)-f(1)=f(1)-f(0)-f(1)=-f(0)=-3
故答案为:-3.
点评 本题考查了抽象函数及其应用,函数的求值问题.解题的关键是发现其周期性的规律,进而转化求解


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
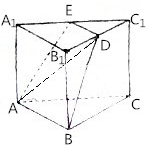 如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=2,AA1=$\sqrt{2}$,E是A1C1边的中点,过A,B,E作截面交B1C1于点D
如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=2,AA1=$\sqrt{2}$,E是A1C1边的中点,过A,B,E作截面交B1C1于点D查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,$∠ACB={90°},AC=1,CB=\sqrt{2}$,侧棱AA1=1,侧面AA1B1B的两条对角线交于点D,B1C1的中点为M.
如图,直三棱柱ABC-A1B1C1中,$∠ACB={90°},AC=1,CB=\sqrt{2}$,侧棱AA1=1,侧面AA1B1B的两条对角线交于点D,B1C1的中点为M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
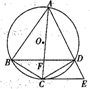 如图,ABCD是圆O的内接四边形,点C是$\widehat{BD}$的中点,切线CE交AD的延长线于E,AC交BD于F.
如图,ABCD是圆O的内接四边形,点C是$\widehat{BD}$的中点,切线CE交AD的延长线于E,AC交BD于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,D为AB的中点,点E,点F分别在BC和B1B上,且直线DE∥平面A1C1F,B1D⊥A1F,AC⊥AB.
如图,在直三棱柱ABC-A1B1C1中,D为AB的中点,点E,点F分别在BC和B1B上,且直线DE∥平面A1C1F,B1D⊥A1F,AC⊥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com