
���� ��1�����ݵ����ļ������弴�������
��2�����ú��������Ժ͵���֮��Ĺ�ϵ������⼴�ɣ�
��3���������h��x���ı���ʽ���������h��x���ĵ��������ú�����ֵ����ֵ�͵���֮��Ĺ�ϵ������⣮
��� �⣺��1����f��x��=blnx+x-$\frac{1}{x}$��x��0��
��f�䣨x��=$\frac{b}{x}$+1+$\frac{1}{{x}^{2}}$��
��f�䣨1��=b+2��
������y=f��x���ڵ㣨1��2������������ֱ��x-y+3=0��ֱ��
��b+2=-1��
��b=-3��
��2���ߺ���f��x����[1��+�ޣ��ϵ���������
��f�䣨x��=$\frac{b}{x}$+1+$\frac{1}{{x}^{2}}$��0����[1��+�ޣ��Ϻ������
��b��-x-$\frac{1}{x}$����[1��+�ޣ��Ϻ����
��x+$\frac{1}{x}$��2$\sqrt{x•\frac{1}{x}}$=2�����ҽ���x=1ʱȡ�Ⱥţ�
��b��-2��
��b��ȡֵ��ΧΪ[-2��+�ޣ���
��3��h��x��=f��x��+g��x��=lnx+$\frac{1}{2}$x2+tx���䶨����Ϊ��0��+�ޣ���
�ã�h�䣨x��=$\frac{1}{x}$+x+t=$\frac{{x}^{2}+tx+1}{x}$
��h�䣨x��=0�����ֱ�Ϊx1��x2������x1•x2=1��x1+x2=-t��
��x2=$\frac{1}{{x}_{1}}$���Ӷ���m=-x1-$\frac{1}{{x}_{1}}$��
��t��-$\frac{{3\sqrt{2}}}{2}$��x1��x2��
��x1��[$\frac{\sqrt{2}}{2}$��1]
��h��x1��-h��x2��=h��x1��-h��$\frac{1}{{x}_{1}}$��=2lnx1+��x12-$\frac{1}{{x}_{1}^{2}}$��+��-x1-$\frac{1}{{x}_{1}}$����x1-$\frac{1}{{x}_{1}}$����
��գ�x��=2lnx-��x2-$\frac{1}{{x}^{2}}$����x��[$\frac{\sqrt{2}}{2}$��1]��
��[h��x1��-h��x2��]min=�գ�x��min��
�ա䣨x��=-$\frac{��{x}^{2}-1��^{2}}{{x}^{3}}$��
��x�ʣ�$\frac{\sqrt{2}}{2}$��1]ʱ���ա䣨x����0��
��գ�x����[$\frac{\sqrt{2}}{2}$��1]�ϵ����ݼ���
�գ�x��min=�գ�1��=0��
��h��x1��-h��x2������СֵΪ0��
���� ������Ҫ���麯�������ԣ���ֵ����ֵ�͵����Ĺ�ϵ�������ĵ��������ù��취�ǽ������Ĺؼ����ۺ��Խ�ǿ����һ�����Ѷȣ�


 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
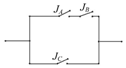 ��ͼ��JA��JB�������ش������뿪��JC��������ij��ʱ����ÿ�������ܹ��պϵĸ��ʶ���0.5�����������ʱ������·���������ĸ���Ϊ0.625��
��ͼ��JA��JB�������ش������뿪��JC��������ij��ʱ����ÿ�������ܹ��պϵĸ��ʶ���0.5�����������ʱ������·���������ĸ���Ϊ0.625���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {2} | B�� | {0��2} | C�� | {-1��2} | D�� | {-1��0��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\frac{3}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | c��a��b | C�� | b��c��a | D�� | b��a��c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | c��a��b | C�� | c��b��a | D�� | b��c��a |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com