
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | 3 |
分析 由正弦定理将2ccosB=2a+b,转化成2sinC•cosB=2sin A+sinB,由三角形内角和定理,将sin A=sin(B+C),利用两角和的正弦公式展开,化简求得,
sinC的值,由余弦定理、三角形的面积公式及基本不等式关系,求得ab的最小值.
解答 解:由正弦定理,有$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,又2c•cosB=2a+b,得
2sinC•cosB=2sin A+sinB,
由A+B+C=π,得sin A=sin(B+C),
则2sinC•cosB=2sin(B+C)+sinB,即2sinB•cosC+sinB=0,
又0<B<π,sinB>0,得cosC=-$\frac{1}{2}$,
因为0<C<π,得C=$\frac{2π}{3}$,
则△ABC的面积为S△=$\frac{1}{2}$ab sinC=$\frac{\sqrt{3}}{4}$ab,即c=3ab,
由余弦定理,得c2=a2+b2-2ab cosC,化简,得a2+b2+ab=9a2b2,
∵a2+b2≥2ab,当仅当a=b时取等号,
∴2ab+ab≤9a2b2,即ab≥$\frac{1}{3}$,故ab的最小值是$\frac{1}{3}$.
故答案选:B.
点评 本题考查正余弦定理、三角形内角和定理及基本不等式相结合,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | |
| A型数量(台) | 11 | 10 | 15 | A4 | A5 |
| B型数量(台) | 9 | 12 | 13 | B4 | B5 |
| C型数量(台) | 15 | 8 | 12 | C4 | C5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -240 | C. | -480 | D. | 960 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:解答题
如图,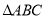 和
和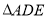 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形, ,点
,点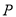 为射线
为射线 与射线
与射线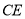 的交点.
的交点.
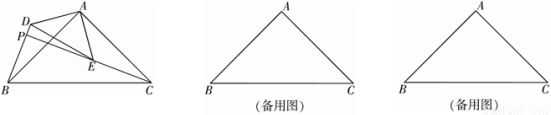
(1)求证: ;
;
(2)若 ,把
,把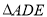 绕点
绕点 旋转,
旋转,
①当 时,求
时,求 的长;
的长;
②直接写出旋转过程中线段 长的最小值与最大值.
长的最小值与最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
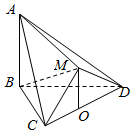 如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com