Question

【题目】在四棱锥中，四边形是矩形，平面 平面，点、分别为、中点.

（1）求证： 平面；

（2）若，求平面DEF与平面所成锐二面角的余弦值.

Answer 1

【答案】（1）见解析（2）

【解析】试题分析：（I）取中点，连接．可证得四边形是平行四边形， ，

而平面， 平面，有平面

（II）取中点，连接，证明，以为原点，OA,OP为x,y轴

建立空间直角坐标系，用向量法求解即可.

试题解析：（I）证明：取中点，连接．

在△中，有

分别为、中点

在矩形中， 为中点

四边形是平行四边形

而平面， 平面

平面

（II）取中点，连接，设.

四边形是矩形

平面 平面,平面 平面= ， 平面

平面

又 ， ， 为中点

， ， .

故可建立空间直角坐标系，如图所示，则

， ， ， ，

，

，

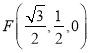设是平面的一个法向量，则

，即

不妨设，则．

易知向量为平面的一个法向量．

故平面与平面所成锐二面角的余弦值为.