
【题目】如图,已知点![]() ,
,![]() 是以
是以![]() 为底边的等腰三角形,点
为底边的等腰三角形,点![]() 在直线
在直线![]() :
:![]() 上.
上.

(1)求![]() 边上的高
边上的高![]() 所在直线的方程;
所在直线的方程;
(2)求![]() 的面积.
的面积.
【答案】解:(Ⅰ)由题意可知,E为AB的中点,∴E(3,2),……………………1分
且![]() ,……………………………………………………1分,
,……………………………………………………1分,
∴CE:y-2=x-3,即x-y-1=0.………………………………2分
(Ⅱ)由![]() 得C(4,3),…………………………………1分
得C(4,3),…………………………………1分
∴|AC|=|BC|=2,AC⊥BC,…………………………………………1分
∴![]()
【解析】
试题分析:
(1)由题意,求得直线![]() 的斜率,从而得到
的斜率,从而得到![]() ,利用直线的点斜式方程,即可求解直线
,利用直线的点斜式方程,即可求解直线![]() 的方程;
的方程;
(2)由![]() ,求得
,求得![]() ,利用两点间的距离公式和三角形的面积公式,即可求得三角形的面积.
,利用两点间的距离公式和三角形的面积公式,即可求得三角形的面积.
试题解析:
(Ⅰ)由题意可知,![]() 为
为![]() 的中点,
的中点,![]()
∴![]() ,且
,且![]() ,
,
∴![]() 所在直线方程为
所在直线方程为![]() ,
,
即![]() .
.
(Ⅱ)由![]() 得
得![]()
∴![]()
∴![]() ,
,![]()
∴![]()
∴![]()


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知关于![]() 的一次函数
的一次函数![]()
(1)设集合![]() 和
和![]() 分别从集合
分别从集合![]() 和
和![]() 中随机取一个数作为
中随机取一个数作为![]() 和
和![]() ,求函数
,求函数![]() 是增函数的概率;
是增函数的概率;
(2)实数![]() 满足条件
满足条件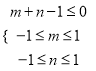 求函数
求函数![]() 的图象经过一、二、三象限的概率.
的图象经过一、二、三象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市若规划一居民小区ABCD,AD=2千米,AB=1千米,∠A=90°,政府决定从该地块中划出一个直角三角形地块AEF建活动休闲区(点E,F分别在线段AB,AD上),且该直角三角形AEF的周长为1千米,△AEF的面积为S. 
(1)①设AE=x,求S关于x的函数关系式;
②设∠AEF=θ,求S关于θ的函数关系式;
(2)试确定点E的位置,使得直角三角形地块AEF的面积S最大,并求出S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com