
分析 (1)把a=b=1代入f(x),化简得3•(3x)2+2•3x-1=0,求解即可得答案;
(2)①f(x)是奇函数,得f(-x)+f(x)=0,代入原函数求解得a,b的值,判断函数f(x)的单调性,不等式f(t2-2t)<f(2t2-k)恒成立,由函数的单调性可得k的取值范围;
②由f(x)•[g(x)+2]=$\frac{1}{3}$(3-x-3x),化简得不等式g(2x)≥m•g(x)-11恒成立,然后构造函数和由函数f(x)的单调性即可求得实数m的最大值.
解答 解:(1)由题意,$\frac{-{3}^{x}+1}{{3}^{x+1}+1}={3}^{x}$,化简得3•(3x)2+2•3x-1=0,
解得3x=-1(舍)或${3}^{x}=\frac{1}{3}$,
∴x=-1;
(2)∵f(x)是奇函数,
∴f(-x)+f(x)=0,
∴$\frac{-{3}^{-x}+a}{{3}^{-x+1}+b}+\frac{-{3}^{x}+a}{{3}^{x+1}+b}=0$,
化简并变形得:(3a-b)(3x+3-x)+2ab-6=0,
要使上式对任意的x成立,则3a-b=0且2ab-6=0,
解得:$\left\{\begin{array}{l}{a=1}\\{b=3}\end{array}\right.$或$\left\{\begin{array}{l}{a=-1}\\{b=-3}\end{array}\right.$,
∵f(x)的定义域是R,
∴$\left\{\begin{array}{l}{a=-1}\\{b=-3}\end{array}\right.$,(舍去)
∴a=1,b=3,∴$f(x)=\frac{-{3}^{x}+1}{{3}^{x+1}+3}$.
①$f(x)=\frac{-{3}^{x}+1}{{3}^{x+1}+3}$=$\frac{1}{3}(-1+\frac{2}{{3}^{x}+1})$对任意x1,x2∈R,x1<x2有:
$f({x}_{1})-f({x}_{2})=\frac{1}{3}(\frac{2}{{3}^{{x}_{1}}+1}-\frac{2}{{3}^{{x}_{2}}+1})$=$\frac{2}{3}[\frac{{3}^{{x}_{2}}-{3}^{{x}_{1}}}{({3}^{{x}_{1}}+1)({3}^{{x}_{2}}+1)}]$,
∵x1<x2,∴${3}^{{x}_{2}}-{3}^{{x}_{1}}>0$,∴f(x1)>f(x2),
因此f(x)在R上递减.
∵f(t2-2t)<f(2t2-k),
∴t2-2t>2t2-k,
即t2+2t-k<0在t∈R时有解
∴△=4+4k>0,解得:k>-1,
∴k的取值范围为(-1,+∞);
②∵f(x)•[g(x)+2]=$\frac{1}{3}$(3-x-3x),
∴$g(x)=\frac{{3}^{-x}-{3}^{x}}{3f(x)}-2$即g(x)=3x+3-x,
∴g(2x)=32x+3-2x=(3x+3-x)2-2,
不等式g(2x)≥m•g(x)-11恒成立,
即(3x+3-x)2-2≥m•(3x+3-x)-11,
即:$m≤{3}^{x}+{3}^{-x}+\frac{9}{{3}^{x}+{3}^{-x}}$恒成立.
令t=3x+3-x,t≥2,则$m≤t+\frac{9}{t}$在t≥2时恒成立,
令$h(t)=t+\frac{9}{t}$,${h}^{′}(t)=1-\frac{9}{{t}^{2}}$,
t∈(2,3)时,h′(t)<0,∴h(t)在(2,3)上单调递减,
t∈(3,+∞)时,h′(t)>0,∴h(t)在(3,+∞)上单调递增,
∴h(t)min=h(3)=6,∴m≤6.
∴实数m的最大值为6.
点评 本题考查函数的奇偶性和单调性的运用,考查不等式恒成立问题,注意运用参数分离,转化为求最值问题,考查运算能力,属于难题.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
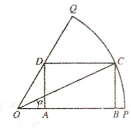 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,则矩形ABCD的面积最大是$\frac{\sqrt{3}}{6}$.
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形.记∠COP=α,则矩形ABCD的面积最大是$\frac{\sqrt{3}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -2 | C. | 4 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com