
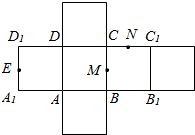
 如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,
如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,分析 (Ⅰ)根据该正方体的平面展开图及斜二测画法即可作出该正方体的水平放置的直观图;
(Ⅱ)根据中位线的性质便有MN∥BC1,从而得出MN∥平面BEC1,可以说明四边形BMD1E为平行四边形,从而得到MD1∥平面BEC1,从而由面面平行的判定定理即可得出平面BEC1∥平面D1MN.
解答 解:(Ⅰ)该正方体的水平放置直观图如下图所示: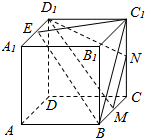
(Ⅱ)证明:M,N分别为BC,CC1的中点;
∴MN∥BC1,BC1?平面BEC1,MN?平面BEC1;
∴MN∥平面BEC1;
又E为A1D1中点;
∴ED1∥BM,且ED1=BM;
∴四边形BMD1E为平行四边形;
∴MD1∥BE;
∴MD1∥平面BEC1,MN∩MD1=M;
∴平面BEC1∥平面D1MN.
点评 考查正方体的水平放置的直观图的画法,由立体图形的平面展开图,可以画出其水平放置的直观图,以及中位线的性质,线面平行的判定定理,平行四边形的判定,面面平行的判定定理.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24种 | B. | 48种 | C. | 36种 | D. | 28种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 5+4$\sqrt{3}$ | C. | 7 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
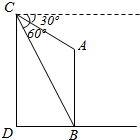 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )| A. | 30m | B. | 20$\sqrt{3}$m | C. | $\frac{40\sqrt{3}}{3}$m | D. | 40m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
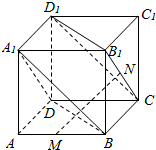 如图,正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.
如图,正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com