
分析 由函数有极值可得b<a2,由定积分可求满足题意的区域面积,由几何概型的概率公式可得.由函数有极值可得b<a2,由定积分可求满足题意的区域面积,由几何概型的概率公式可得.
解答 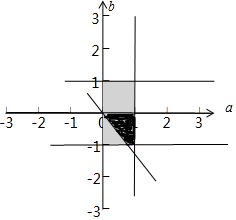 解:对y=$\frac{1}{3}$ax3+ax2+b求导数可得y′=ax2+2ax,令ax2+2ax=0,可得x=0,或x=-2,0<a<1,
解:对y=$\frac{1}{3}$ax3+ax2+b求导数可得y′=ax2+2ax,令ax2+2ax=0,可得x=0,或x=-2,0<a<1,
x=-2是极大值点,x=0是极小值点,函数y=$\frac{1}{3}$ax3+ax2+b
有三个零点,可得$\left\{\begin{array}{l}{f(-2)>0}\\{f(0)<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-\frac{8}{3}a+4a+b>0}\\{b<0}\end{array}\right.$,
画出可行域如图:满足函数y=$\frac{1}{3}$ax3+ax2+b有三个零点,如图深色区域,实数a,b满足0<a<1,-1<b<1,为长方形区域,所以长方形的面积为:2,实数区域的面积为:$\frac{1}{2}$×(1+$\frac{1}{4}$)=$\frac{5}{8}$
∴所求概率为P=$\frac{\frac{5}{8}}{2}$=$\frac{5}{16}$,
故答案为:$\frac{5}{16}$.
点评 本题考查几何概型的求解,涉及导数求解函数的极值,函数的零点以及线性规划的应用,属中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:高中数学 来源: 题型:解答题
 18、甲、乙两位同学参加数学文化知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
18、甲、乙两位同学参加数学文化知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
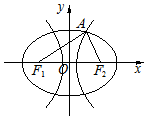 如图,椭圆与双曲线有公共焦点F1,F2,它们在第一象限的交点为A,且AF1⊥AF2
如图,椭圆与双曲线有公共焦点F1,F2,它们在第一象限的交点为A,且AF1⊥AF2| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{14}{15}$ | B. | $\frac{1}{15}$ | C. | .$\frac{3}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | A1 | A2 | A3 | A4 | A5 |
| 评价指数(x,y,z) | (3,4,3) | (4,3,4) | (4,4,2) | (4,3,5) | (4,5,4) |
| 学生编号 | B1 | B2 | B3 | B4 | B5 |
| 评价指数(x,y,z) | (3,5,3) | (4,3,2) | (5,4,4) | (5,4,5) | (4,5,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com