
分析 (Ⅰ)对函数求导,分类讨论n的取值,根据函数的单调性及极值情况即可判断;
(Ⅱ)利用数学归纳法,构造函数,求导根据函数的单调性,比较自变量的大小.
解答 解:(Ⅰ)f′(x)=(a-x)ex-ex=(a-x-1)ex,令f′(x)=0
解得:x=a-1,
当a-1≤0时,f′(x)≤0,在x>0时恒成立,
∴f(x)在上(0,+∞)单调递减;
∴f(x)<f(0)=a-1≤0,即当x>0时,f(x)<0,成立,
当a-1>0时,函数f(x)在(0,a-1)上单调递减增,在(a-1,+∞)单调递减;
∴?x0=a-1>0,f(x0)>f(0)=a-1>0,
与x>0时,f(x)<0矛盾,以实数a的最大值为1;
(Ⅱ)证明:xn+1>$\frac{1}{{2}^{n}}$,
当n=1时,${e}^{{x}_{2}}$=$\frac{{e}^{{x}_{1}}-1}{{x}_{1}}$=e-1>$\sqrt{e}$,
∴x2>$\frac{1}{2}$,显然成立,
假设当n=k时,(k∈N*),xk+1>$\frac{1}{{2}^{k}}$,
${e}^{{x}_{k+2}}$=g(xk+1)>g($\frac{1}{{2}^{k}}$),下证g($\frac{1}{{2}^{k}}$)≥$e\frac{1}{{2}^{k+1}}$=${e}^{\frac{1}{2}•\frac{1}{{2}^{k}}}$,
构造函数h(x)=x(g(x)-${e}^{\frac{x}{2}}$),
则h′(x)=ex-(1+$\frac{x}{2}$)${e}^{\frac{x}{2}}$=${e}^{\frac{x}{2}}$[${e}^{\frac{x}{2}}$-(1+$\frac{x}{2}$)]>0,
∴h(x)在(0,+∞)是增函数,
h($\frac{1}{{2}^{k}}$)>0,
∴g($\frac{1}{{2}^{k}}$)>$\frac{1}{{e}^{{2}^{k+1}}}$,
∴${e}^{{x}_{k+1}}$>$\frac{1}{{e}^{{2}^{k+1}}}$,xk+1>$\frac{1}{{2}^{k+1}}$,
由数学归纳法可知:对于正整数n,xn>$\frac{1}{{2}^{n}}$,
由(1)可知:a=1时,x>0,f(x)<0,
f(xn)=(1-xn)${e}^{{x}_{n}-1}$<0,xn•${e}^{{x}_{n}}$>${e}^{{x}_{n}}$-1=xn•${e}^{{x}_{n+1}}$,
∴${e}^{{x}_{n}}$>en+1,即xn+1<xn,
∴${x_n}>{x_{n+1}}>\frac{1}{2^n}({n∈{N^*}})$.
点评 本题考查利用导数求函数的单调性,利用构造法即数学归纳法证明不等式成立,考查转化思想,考查分析问题及解决问题的能力,属于中档题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
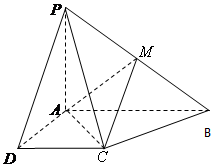 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com