
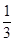 AC,AE=
AC,AE=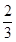 AB,BD,CE相交于点F.
AB,BD,CE相交于点F.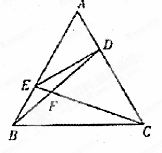
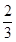 .
.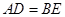 ,再利用三角形相似,得出
,再利用三角形相似,得出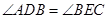 ,所以
,所以 ,所以可证
,所以可证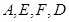 四点共圆;第二问,根据所给正三角形的边长为2,利用已知的比例关系,得出各个小边的长度,从而得出
四点共圆;第二问,根据所给正三角形的边长为2,利用已知的比例关系,得出各个小边的长度,从而得出 为正三角形,所以得出
为正三角形,所以得出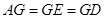 ,所以
,所以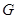 是
是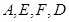 所在圆的圆心,而
所在圆的圆心,而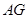 是半径,即为
是半径,即为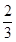 .
.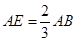 , ∴
, ∴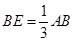 ,
, 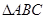 中,
中, 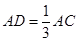 , ∴
, ∴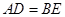 ,
, 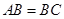 ,
,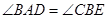 , ∴
, ∴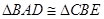 , ∴
, ∴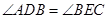 ,
,  ,所以
,所以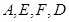 四点共圆. 5分
四点共圆. 5分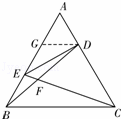
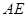 的中点
的中点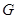 ,连接
,连接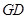 ,则
,则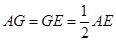 ,
, 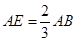 , ∴
, ∴ ,
, 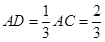 ,
,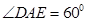 , ∴
, ∴ 为正三角形,
为正三角形, 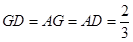 ,即
,即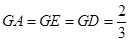 ,
, 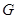 是
是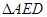 外接圆的圆心,且圆
外接圆的圆心,且圆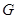 的半径为
的半径为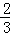 .
. 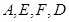 四点共圆,即
四点共圆,即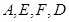 四点共圆
四点共圆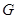 ,其半径为
,其半径为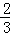 . 10分
. 10分

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
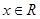 ,
,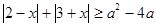 恒成立,则
恒成立,则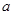 满足________.
满足________.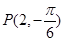 到直线
到直线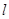 :
: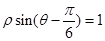 的距离是_______.
的距离是_______.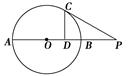
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com