

| A. | $\frac{3}{4}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$ | B. | $\frac{5}{12}$$\overrightarrow{b}$-$\frac{3}{4}$$\overrightarrow{a}$ | C. | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | D. | $\frac{5}{12}$$\overrightarrow{a}$-$\frac{3}{4}$$\overrightarrow{b}$ |
分析 根据向量的三角形法和加减的几何意义即可求出.
解答 解:∵$\overrightarrow{BC}$=4$\overrightarrow{BD}$,
∴$\overrightarrow{DC}$=$\frac{3}{4}$$\overrightarrow{BC}$=$\frac{3}{4}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)
∴$\overrightarrow{DE}$=$\overrightarrow{DC}$+$\overrightarrow{CE}$=$\frac{3}{4}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)+$\frac{1}{3}$$\overrightarrow{CA}$=($\frac{3}{4}$-$\frac{1}{3}$)$\overrightarrow{AC}$-$\frac{3}{4}$$\overrightarrow{AB}$=$\frac{5}{12}$$\overrightarrow{b}$-$\frac{3}{4}$$\overrightarrow{a}$,
故选:B
点评 本题考查了向量的三角形法和向量的数乘运算,属于基础题


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:解答题
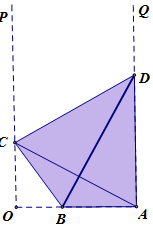 在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图OP∥AQ,OA⊥AQ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知OA=2,
在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图OP∥AQ,OA⊥AQ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知OA=2,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 |
| y | 0.5 | 1 | 1.5 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{5}$ | B. | $8\sqrt{5}$ | C. | $10\sqrt{5}$ | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -π | B. | -$\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com