练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．若函数f（x）=cos（2x+φ）是奇函数，则φ可取一个值为（　　）
    A．-πB．-$\frac{π}{2}$C．$\frac{π}{4}$D．2π

    分析 利用诱导公式，三角函数的奇偶性，求得φ的值．

    解答 解：∵函数f（x）=cos（2x+φ）是奇函数，∴φ=kπ+$\frac{π}{2}$，k∈Z，
    故当k=-1时，φ=-$\frac{π}{2}$，
    故选：B．

    点评 本题主要考查诱导公式，三角函数的奇偶性，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．如图，已知$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，$\overrightarrow{BC}$=4$\overrightarrow{BD}$，$\overrightarrow{CA}$=3$\overrightarrow{CE}$，则$\overrightarrow{DE}$=（　　）
    A．$\frac{3}{4}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$B．$\frac{5}{12}$$\overrightarrow{b}$-$\frac{3}{4}$$\overrightarrow{a}$C．$\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$D．$\frac{5}{12}$$\overrightarrow{a}$-$\frac{3}{4}$$\overrightarrow{b}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知向量$\overrightarrow{m}$=（a，b2-b+$\frac{7}{3}$），$\overrightarrow{n}$=（a+b+2，1），$\overrightarrow{μ}$=（2，1）．
    （1）若$\overrightarrow{m}$∥$\overrightarrow{μ}$，求a的最小值；
    （2）求证：$\overrightarrow{m}$ 与$\overrightarrow{n}$的夹角不是钝角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

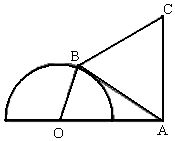    8．如图，半圆O的直径为2，A为直径延长线上的一点，OA=2，B为半圆上任意一点，以AB为一边作等边三角形ABC．当四边形OACB面积最大时，∠AOB=150°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．当x+y+z=1时，则x2+y2+z2的最小值为（　　）
    A．$\frac{1}{3}$B．$\frac{1}{9}$C．$\frac{1}{27}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．以下判断正确的是（　　）
    A．命题p是真命题时，命题“p∧q”一定是真命题
    B．命题“p∧q”是真命题时，命题p一定是真命题
    C．命题“p∧q”是假命题时，命题p一定是假命题
    D．命题p是假命题时，命题“p∧q”不一定是假命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．下面的茎叶图记录了甲、乙两名同学在10次英语听力比赛中的成绩（单位：分），已知甲得分的中位数为76分，乙得分的平均数是75分，则下列结论正确的是（　　）
    A．$\overline{x_甲}=76，\overline{x_乙}=75$B．乙同学成绩较为稳定
    C．甲数据中x=3，乙数据中y=6D．甲数据中x=6，乙数据中y=3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

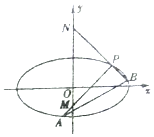    9．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{3}}}{2}$，以椭圆的四个顶点为顶点的四边形的面积为8．
    （1）求椭圆C的方程；
    （2）如图，斜率为$\frac{1}{2}$的直线l与椭圆C交于A，B两点，点P（2，1）在直线l的上方，若∠APB=90°，且直线PA，PB分别与y轴交于点M，N，求线段MN的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．下列命题中：
    ①若x2-3x+2=0，则x=1或x=2       
    ②若-2≤x≤3，则（x+2）（x-3）≤0
    ③若x=y=0，则x2+y2=0
    ④若x、y∈N*，x+y是奇数，则x、y中一个是奇数，一个是偶数．
    那么（　　）
    A．①的逆命题为真B．②的否命题为假C．③的逆否命题为假D．④的逆命题为假

    查看答案和解析>>

    同步练习册答案