
分析 (1)由$\overrightarrow{m}$∥$\overrightarrow{μ}$,利用向量平行的性质得到a=2(${b}^{2}-b+\frac{7}{3}$)=2($b-\frac{1}{2}$)2+$\frac{25}{6}$,由此能求出a的最小值.
(2)利用向量的数量积求出$\overrightarrow{m}•\overrightarrow{n}$=${a}^{2}+(b+2)a+{b}^{2}-b+\frac{7}{3}$,从而$\overrightarrow{m}•\overrightarrow{n}$是关于a的二次函数,利用根的差别式推导出$\overrightarrow{m}•\overrightarrow{n}$≥0恒成立,由此能证明$\overrightarrow{m},\overrightarrow{n}$的夹角不是钝角.
解答 解:(1)∵向量$\overrightarrow{m}$=(a,b2-b+$\frac{7}{3}$),$\overrightarrow{μ}$=(2,1),$\overrightarrow{m}$∥$\overrightarrow{μ}$,
∴由题意得a=2(${b}^{2}-b+\frac{7}{3}$)=2($b-\frac{1}{2}$)2+$\frac{25}{6}$,
∴当b=$\frac{1}{2}$时,a取最小值amin=$\frac{25}{6}$.
证明:(2)∵向量$\overrightarrow{m}$=(a,b2-b+$\frac{7}{3}$),$\overrightarrow{n}$=(a+b+2,1),
∴$\overrightarrow{m}•\overrightarrow{n}$=a(a+b+2)+${b}^{2}-b+\frac{7}{3}$
=${a}^{2}+(b+2)a+{b}^{2}-b+\frac{7}{3}$,
∴$\overrightarrow{m}•\overrightarrow{n}$是关于a的二次函数,
∵$△=(b+2)^{2}-4({b}^{2}-b+\frac{7}{3})$=-3b2+8b-$\frac{16}{3}$=-3(b-$\frac{4}{3}$)2≤0,
∴$\overrightarrow{m}•\overrightarrow{n}$≥0恒成立,
故$\overrightarrow{m},\overrightarrow{n}$的夹角不是钝角.
点评 本题考查实数的最小值的求法,考查两向量的夹角不是钝角的证明,考查向量平行、向量的数量积、二次函数、根的判别式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:解答题
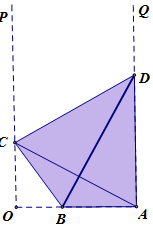 在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图OP∥AQ,OA⊥AQ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知OA=2,
在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图OP∥AQ,OA⊥AQ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知OA=2,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{5}$ | B. | $8\sqrt{5}$ | C. | $10\sqrt{5}$ | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -π | B. | -$\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com