练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．巴西医生马廷恩收集犯有各种贪污、受贿罪的官员与廉洁官员寿命的调查资料：500名贪官中有340人的寿命小于平均寿命，160人的寿命大于或等于平均寿命；590名廉洁官员中有90人的寿命小于平均寿命，500人的寿命大于或等于平均寿命．这里，平均寿命是指“当地人均寿命”． 根据以上数据列2×2列联表，并用独立性检验的方法判断能否在犯错误的概率不超过0.01的前提下认为官员在经济上是否清廉与他们寿命的长短之间有关系？

    分析 先作出2×2列联表，再计算K2，与临界值比较，即可得到结论．

    解答 解：据题意列2×2列联表如下：

    短寿（B）长寿（$\overline{B}$）总计
    贪官（A）340160500
    廉洁官（$\overline{A}$）90500590
    总计4306601 090
    -----------------------（3分）
    假设官员是否清廉与他们寿命的长短无关．-----------------------（4分）
    由公式得K2的观测值$k=\frac{{1090×{{（340×500-160×90）}^2}}}{500×590×430×660}≈315.218$-----------------------（8分）
    因为315.218＞6.635，因此，在犯错误的概率不超过0.01的前提下认为官员在经济上是否清廉与他们寿命的长短之间是有关系的．-----------------------（10分）

    点评 本题考查独立性检验知识，考查学生的计算能力，考查学生分析解决问题的能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    11．已知向量$\overrightarrow{m}$=（a，b2-b+$\frac{7}{3}$），$\overrightarrow{n}$=（a+b+2，1），$\overrightarrow{μ}$=（2，1）．
    （1）若$\overrightarrow{m}$∥$\overrightarrow{μ}$，求a的最小值；
    （2）求证：$\overrightarrow{m}$ 与$\overrightarrow{n}$的夹角不是钝角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．下面的茎叶图记录了甲、乙两名同学在10次英语听力比赛中的成绩（单位：分），已知甲得分的中位数为76分，乙得分的平均数是75分，则下列结论正确的是（　　）
    A．$\overline{x_甲}=76，\overline{x_乙}=75$B．乙同学成绩较为稳定
    C．甲数据中x=3，乙数据中y=6D．甲数据中x=6，乙数据中y=3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

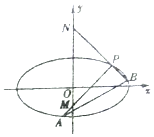    9．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{3}}}{2}$，以椭圆的四个顶点为顶点的四边形的面积为8．
    （1）求椭圆C的方程；
    （2）如图，斜率为$\frac{1}{2}$的直线l与椭圆C交于A，B两点，点P（2，1）在直线l的上方，若∠APB=90°，且直线PA，PB分别与y轴交于点M，N，求线段MN的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．函数$f（x）=\frac{1}{x^2}+2x（x＞0）$的最小值为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．如图，在各棱长为2的三棱柱ABC-A1B1C1中，侧面A1ACC1⊥底面ABC，∠A1AC=60°．
    （1）求三棱柱ABC-A1B1C1的体积；
    （2）已知点D是平面ABC内一点，且四边形ABCD为平行四边形，在直线AA1上是否存在点P，使DP∥平面AB1C？若存在，请确定点P的位置，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．在空间直角坐标系Oxyz中，已知A（1，-2，3），B（2，1，-1），若直线AB交平面yoz于点C，则点C的坐标为（0，-5，-5）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．下列命题中：
    ①若x2-3x+2=0，则x=1或x=2       
    ②若-2≤x≤3，则（x+2）（x-3）≤0
    ③若x=y=0，则x2+y2=0
    ④若x、y∈N*，x+y是奇数，则x、y中一个是奇数，一个是偶数．
    那么（　　）
    A．①的逆命题为真B．②的否命题为假C．③的逆否命题为假D．④的逆命题为假

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．函数f（x）=x3-3x2在区间[-2，4]上的最大值为（　　）
    A．-4B．0C．16D．20

    查看答案和解析>>

    同步练习册答案