练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．某几何体的三视图如图所示，则该几何体的外接球的表面积为50π．

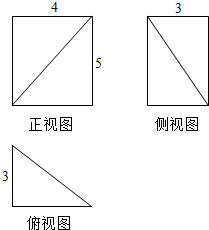
    分析 由已知中的三视图可得：该几何体是一个以俯视图为底面的三棱柱切去一个三棱锥所得的组合体，求出三棱锥的外接球半径，代入球表面积公式，可得答案．

    解答 解：由已知中的三视图可得：该几何体是一个以俯视图为底面的三棱锥柱切去一个三棱锥所得的组合体，
    其外接球，即以俯视图为底面的三棱锥柱的外接球，
    由已知得：底面外接圆的半径r=$\frac{1}{2}\sqrt{{3}^{2}+{4}^{2}}$=$\frac{5}{2}$，
    球心到底面的距离d=$\frac{5}{2}$，
    故球的半径R=$\frac{5}{2}$$\sqrt{2}$，
    故球的表面积S=50π，
    故答案为：50π

    点评 本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．已知椭圆$\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{16}$=1，其长轴两端点与双曲线两焦点重合，而双曲线的两个顶点又是椭圆的焦点．求此双曲线的标准方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知f（x）是定义在R上的奇函数，且当x＜0时，$f（x）=2_{\;}^x$，则f（log23）的值为（　　）
    A．-3B．$-\frac{1}{3}$C．$\frac{1}{3}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的左右焦点分别是F1，F2，若以线段F1F2为直径的圆与椭圆有交点，则椭圆C的离心率的取值范围是$\frac{\sqrt{2}}{2}$≤e＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．现有A，B，C三种产品需要检测，产品数量如下表：
    产品ABC
    数量8008001200
    已知采用分层抽样的方法从以上产品中共抽取了7件．
    （1）求分别抽取的三种产品件数；
    （2）已知被抽取的A，B，C三种产品中，一等品分别有1件、2件、2件，现再从已抽取的A，B，C三件产品中各抽取1件，求3件产品都是一等品的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．设有一组圆Ck：（x-k+1）2+（y-3k）2=2k2（k∈N*）．下列四个命题：
    ①存在一条定直线与所有的圆均相切；
    ②存在一条定直线与所有的圆均相交；
    ③存在一条定直线与所有的圆均不相交；
    ④所有的圆均不经过原点．
    其中真命题的序号是（　　）
    A．①③B．②④C．②③D．③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知函数f（x）=2sin（ωx+$\frac{π}{3}$）在区间（0，π）上存在唯一一个x0∈（0，π），使得f（x0）=1，则
    （　　）
    A．ω的最小值为$\frac{1}{3}$B．ω的最小值为$\frac{1}{2}$C．ω的最大值为$\frac{11}{6}$D．ω的最大值为$\frac{13}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．在一个不透明的袋中有5个形状、大小、质地均相同的小球，小球的编号分别为1，2，3，4，5．
    （1）从袋中随机抽取两个小球；
    ①用列举法写出全部基本事件；
    ②求取出的两个小球编号之和不大于5的概率；
    （2）从袋中随机取一个小球记下它的编号m，再将小球放入袋中，然后再从袋中随机取一个小球，记下它的编号n，求函数f（x）=x2-2$\sqrt{n-1}$•x+m+1无零点的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．2015年高考体检中，某校高三共有学生1000人，检查的身体的某项指标为由低到高的4个等级，具体如下表：
    等级 1级 2级 3级 4级
     人数200 500 200 100
    （1）若按分层抽样的方法从中抽取20人，再从这20人中抽取2人，求这2人的该项身体指标级别至少有1人小于2人的概率；
    （2）若把该校高三学生该项指标中恰好为1级的频率视为概率，从这1000人中任选1人，若其该项指标恰好为1级则结束，否则再选取1人，依次选取，直至找到1人该项指标恰好为1级或选够4人，则结束选取，求结束时选取的人数的分布列与期望．

    查看答案和解析>>

    同步练习册答案