
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PD⊥平面ABCD,AD=1,AB=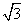 ,BC=4.
,BC=4.
(1)求证:BD⊥PC;
(2)设点E在棱PC上, ,若DE∥平面PAB,求λ的值.
,若DE∥平面PAB,求λ的值.

科目:高中数学 来源: 题型:
圆(x+2)2+y2=5关于直线y=x对称的圆的方程为( )
A.(x-2)2+y2=5 B.x2+(y-2)2=5
C.(x+2)2+(y+2)2=5 D.x2+(y+2)2=5
查看答案和解析>>
科目:高中数学 来源: 题型:
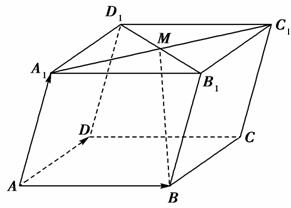
如图,在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若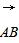 =a,
=a,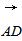 =b,
=b,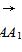 =c,则下列向量中与
=c,则下列向量中与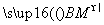 相等的向量是( )
相等的向量是( )
A.-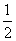 a+
a+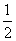 b+c B.
b+c B.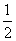 a+
a+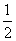 b+c
b+c
C.-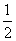 a-
a-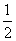 b+c D.
b+c D.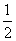 a-
a-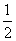 b+c
b+c
查看答案和解析>>
科目:高中数学 来源: 题型:
底面是平行四边形的四棱柱叫平行六面体.如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,N为BB1的靠近B的三等分点,
若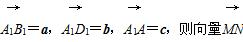 等于( )
等于( )
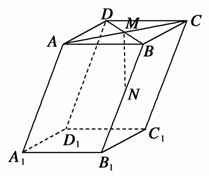
A.-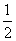 a+
a+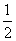 b+
b+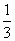 c
c
B.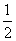 a+
a+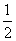 b-
b-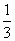 c
c
C.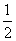 a-
a-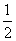 b-
b-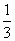 c
c
D.-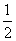 a-
a-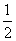 b+
b+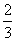 c
c
查看答案和解析>>
科目:高中数学 来源: 题型:
设斜率为2的直线l过抛物线y2=ax(a≠0)的焦点F,且和y轴交于点A.若△OAF(O为坐标原点)的面积为4,则抛物线方程为( )
A.y2=±4x B.y2=±8x
C.y2=4x D.y2=8x
查看答案和解析>>
科目:高中数学 来源: 题型:
问题:①三种不同的容器中分别装有同一型号的零件400个、200个、150个,现在要从这750个零件中抽取一个容量为50的样本;②从20名学生中选出3名参加座谈会.
方法:Ⅰ.随机抽样法 Ⅱ.系统抽样法 Ⅲ.分层抽样法.
其中问题与方法能配对的是( )
A.①Ⅰ,②Ⅱ B.①Ⅲ,②Ⅰ
C.①Ⅱ,②Ⅰ D.①Ⅲ,②Ⅱ
查看答案和解析>>
科目:高中数学 来源: 题型:
已知x与y之间的一组数据:
| x | 0 | 1 | 2 | 3 |
| y | m | 3 | 5.5 | 7 |
已求得y关于x的线性回归方程 =2.1x+0.85,则m的值为( )
=2.1x+0.85,则m的值为( )
A.1 B.0.85
C.0.7 D.0.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com