
分析 求出B={2,3},C={-4,2},由A∩B≠∅与A∩C=∅同时成立.得到3∈A,即9+3a-a2+1=0,由此能求出结果.
解答 解:集合A={x|-x2-ax+a2-1=0},
B={x|x2-5x+6=0}={2,3},C={x|x2+2x-8=0}={-4,2},
∵A∩B≠∅与A∩C=∅同时成立.
∴3∈A,∴9+3a-a2+1=0,
解得a=-2或a=5.
当a=-2时,A={x|x2-2x-3=0}={-1,3},成立;
当a=5时,A={x|x2+5x-24=0}={-8,3},成立.
∴当a为3或5时,A∩B≠∅与A∩C=∅同时成立.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意交集性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
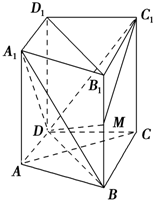 如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1≤x≤3 | B. | x≤-1 | C. | x≥3 | D. | x<-1或x>3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com