
【题目】下列函数中,函数值域为(0,+∞)的是( )
A.y=(x+1)2 , x∈(0,+∞)
B.y=log ![]() x,x∈(1,+∞)
x,x∈(1,+∞)
C.y=2x﹣1
D.y= ![]()
【答案】C
【解析】解:对于A:y=(x+1)2 , x∈(0,+∞),根据二次函数图象及性质可知其值域为(1,+∞);
对于B:y=log ![]() x,x∈(1,+∞),根据对数函数的图象及性质可知,函数是减函数,其值域为(﹣∞,0);
x,x∈(1,+∞),根据对数函数的图象及性质可知,函数是减函数,其值域为(﹣∞,0);
对于C:y=2x﹣1 , 根据指数函数的图象及性质可知,函数是增函数,其值域为(0,+∞);
对于D:y= ![]() ,当x=
,当x= ![]() 时,函数y=0,根据幂函数的图象及性质可知,函数是增函数,其值域为[0,+∞);
时,函数y=0,根据幂函数的图象及性质可知,函数是增函数,其值域为[0,+∞);
故选C.
【考点精析】本题主要考查了函数的值域的相关知识点,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2-5ax+4a2<0(其中a>0),q:实数x满足2<x≤5.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若![]() q是
q是![]() p的必要不充分条件,求实数a的取值范围.
p的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了72名员工进行调查,所得的数据如表所示:
积极支持改革 | 不太支持改革 | 合 计 | |
工作积极 | 28 | 8 | 36 |
工作一般 | 16 | 20 | 36 |
合 计 | 44 | 28 | 72 |
对于人力资源部的研究项目,根据上述数据能得出的结论是
(参考公式与数据: ![]() .当Χ2>3.841时,有95%的把握说事件A与B有关;当Χ2>6.635时,有99%的把握说事件A与B有关; 当Χ2<3.841时认为事件A与B无关.)( )
.当Χ2>3.841时,有95%的把握说事件A与B有关;当Χ2>6.635时,有99%的把握说事件A与B有关; 当Χ2<3.841时认为事件A与B无关.)( )
A.有99%的把握说事件A与B有关
B.有95%的把握说事件A与B有关
C.有90%的把握说事件A与B有关
D.事件A与B无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x|x2﹣3x﹣4≤0},B={x|x2﹣2mx+m2﹣9≤0},C={y|y=ax+b,a>0,且a≠1,x∈R}.
(1)若A∩B=[0,4],求m的值;
(2)若A∩C只有一个子集,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数中,奇函数的个数是( )
①f(x)=ln ![]() ,②g(x)=
,②g(x)= ![]() (ex+e﹣x),③h(x)=lg(
(ex+e﹣x),③h(x)=lg( ![]() ﹣x),④m(x)=
﹣x),④m(x)= ![]() +
+ ![]() .
.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要在墙上开一个上部为半圆,下部为矩形的窗户(如图所示),在窗框总长度为l的条件下, 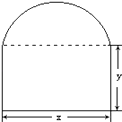
(1)请写出窗户的面积S与圆的直径x的函数关系;
(2)要使窗户透光面积最大,窗户应具有怎样的尺寸?并写出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】衣柜里的樟脑丸会随着时间的挥发而体积缩小,刚放进的新丸体积为a,经过t天后体积V与天数t的关系式为:V=ae﹣kt . 若新丸经过50天后,体积变为 ![]() a,则一个新丸体积变为
a,则一个新丸体积变为 ![]() a需经过的时间为( )
a需经过的时间为( )
A.125天
B.100天
C.50天
D.75天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,任取
,任取![]() ,定义集合:
,定义集合:
![]() ,点
,点![]() ,
, ![]() 满足
满足![]() .
.
设![]() 分别表示集合
分别表示集合![]() 中元素的最大值和最小值,记
中元素的最大值和最小值,记![]() .则
.则
(1) 若函数![]() ,则
,则![]() =______;
=______;
(2)若函数![]() ,则
,则![]() 的最小正周期为______.
的最小正周期为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com