
| A. | 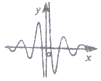 | B. | 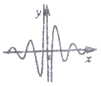 | C. |  | D. |  |
分析 判断函数的奇偶性,并计算特殊值即可得出答案.
解答 解:令f(x)=$\frac{cos6x}{{2}^{x}-{2}^{-x}}$,则f(-x)=$\frac{cos6x}{{2}^{-x}-{2}^{x}}$=-f(x),
∴f(x)是奇函数,图象关于原点对称,排除C,D;
令f(x)=0得cos6x=0,∴6x=$\frac{π}{2}$+kπ,x=$\frac{π}{12}$+$\frac{kπ}{6}$,k∈Z,
∴f(x)的最小正零点为$\frac{π}{12}$,
当x∈(0,$\frac{π}{12}$)时,2x>1>2-x,cos6x>0,∴f(x)>0,排除B,
故选A.
点评 本题考查了函数奇偶性的判断,函数值的计算,余弦函数的性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 320 | B. | 446 | C. | 482 | D. | 248 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
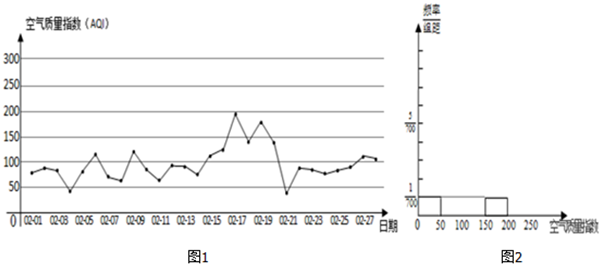
| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 第一组 | 第二组 | 第二组 | 第四组 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 6 | 4 | 22 | 20 |
| 频率 | 0.06 | 0.04 | 0.22 | 0.20 |
| 组号 | 第五组 | 第六组 | 第七组 | 第八组 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 18 | a | 10 | 5 |
| 频率 | b | 0.15 | 0.10 | 0.05 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com