
| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
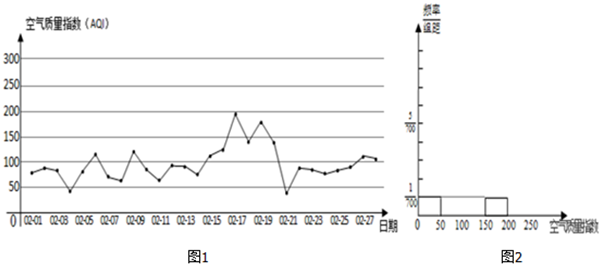
分析 (Ⅰ)由折线图知空气质量指数分别为(0,50],(50,100],(100,150],(150,200]的频数分别为2,16,8,2,由此求出各小矩形的高,从而能补全频率分布直方图,由此能求出该市2月份空气质量指数监测数据的平均数值.
(Ⅱ)该月份该市空气质量为优的有2天,空气质量为良的有16天,由此能求出任取两天至少有一天空气质量为优或良的概率.
(Ⅲ)由已知,该市对环境进行治理,空气质量的均值为E(X)=75,由此能求出该市治理后的空气质量指数大约下降了多少.
解答 解:(Ⅰ)由折线图知空气质量指数分别为(0,50],(50,100],(100,150],(150,200]的频数分别为2,16,8,2,
∴各组对应的频率分布为$\frac{1}{14},\frac{4}{7},\frac{2}{7},\frac{1}{14}$,
∴各小矩形的高分别为$\frac{1}{700},\frac{8}{700},\frac{4}{700},\frac{1}{700}$,
∴补全频率分布直方图,如下图: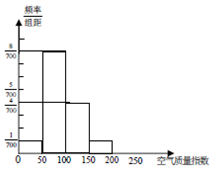
该市2月份空气质量指数监测数据的平均数值为:
$\frac{1}{14}×25+\frac{4}{7}×75+\frac{2}{7}×125+\frac{1}{14}×175$≈92.9.
(Ⅱ)该月份该市空气质量为优的有2天,空气质量为良的有16天,
则任取两天至少有一天空气质量为优或良的概率为p=1-$\frac{{C}_{10}^{2}}{{C}_{28}^{2}}$=$\frac{37}{42}$.
(Ⅲ)由已知,该市对环境进行治理,
该市对环境进行治理,治理后经统计,每天的空气质量指数近似满足X~N(75,552),
空气质量的均值为E(X)=75,
92.9-75=17.9,
故该市治理后的空气质量指数下降了17.9.
点评 本题考查频率分布直方图、折线图、概率等基础知识,考查数据处理能力、运算求解能力,考查化归与转化思想、数形结合思想,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
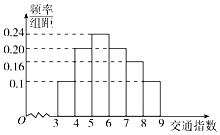 随着社会发展,襄阳市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从襄阳市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:
随着社会发展,襄阳市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从襄阳市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 10 | C. | 9 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,π] | B. | $[{-\frac{π}{2},0}]$ | C. | $[{0,\frac{π}{2}}]$ | D. | [-π,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2-i}{10}$ | B. | $\frac{1+i}{10}$ | C. | $\frac{4+7i}{10}$ | D. | $\frac{4-i}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com