
分析 由题意可得M,Q关于原点对称,即可得到kMN•kQN=$\frac{{b}^{2}}{{a}^{2}}$,分别求出相对应的斜率,再根据离心率公式即可求出
解答  解:由题意可知:M,Q关于原点对称,
解:由题意可知:M,Q关于原点对称,
∴kMN•kQN=$\frac{{b}^{2}}{{a}^{2}}$,
∵kMN=-$\sqrt{3}$,kQN=-$\frac{\sqrt{3}}{3}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=1,
∴e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{2}$
故答案为:$\sqrt{2}$.
点评 本题考查了双曲线的简单性质以及离心率的计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 320 | B. | 446 | C. | 482 | D. | 248 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
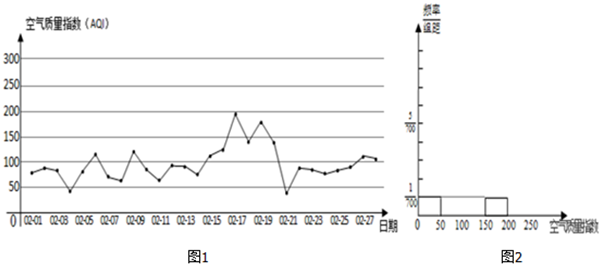
| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
| 男性驾驶人数 | 45 | 10 | 55 |
| 女性驾驶人数 | 25 | 20 | 45 |
| 合计 | 70 | 30 | 100 |
| P(k2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 第一组 | 第二组 | 第二组 | 第四组 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 6 | 4 | 22 | 20 |
| 频率 | 0.06 | 0.04 | 0.22 | 0.20 |
| 组号 | 第五组 | 第六组 | 第七组 | 第八组 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 18 | a | 10 | 5 |
| 频率 | b | 0.15 | 0.10 | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
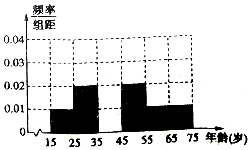 河南多地遭遇年霾,很多学校调整元旦放假时间,提前放假让学生们在家躲霾.郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动Ⅰ级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”.学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成如表:
河南多地遭遇年霾,很多学校调整元旦放假时间,提前放假让学生们在家躲霾.郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动Ⅰ级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”.学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成如表:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com