
分析 (1)利用平面向量的三角形法则和共线原理证明其中两中线的交点在第三条中线上即可;
(2)根据向量的共线原理证明P在三条中线上即可.
解答  (1)证明:在△ABC中,设D、E、F分别为BC、AC、AB的中点,BE与AD的交点为G,
(1)证明:在△ABC中,设D、E、F分别为BC、AC、AB的中点,BE与AD的交点为G,
设$\overrightarrow{BA}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{BC}$=$\overrightarrow{{e}_{2}}$,则$\overrightarrow{CA}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$不共线,
$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}+\overrightarrow{AC}$)=$\frac{1}{2}$$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$,$\overrightarrow{BE}$=$\frac{1}{2}$($\overrightarrow{AB}+\overrightarrow{AC}$)=$\frac{1}{2}\overrightarrow{{e}_{1}}$+$\frac{1}{2}$$\overrightarrow{{e}_{2}}$,
设$\overrightarrow{BG}$=λ$\overrightarrow{BE}$,则$\overrightarrow{AG}$=$\overrightarrow{BG}$-$\overrightarrow{BA}$=λ$\overrightarrow{BE}$-$\overrightarrow{BA}$=($\frac{λ}{2}$-1)$\overrightarrow{{e}_{1}}$+$\frac{λ}{2}$$\overrightarrow{{e}_{2}}$,
∵$\overrightarrow{AG}$,$\overrightarrow{AD}$共线,∴$\frac{-1}{\frac{λ}{2}-1}=\frac{\frac{1}{2}}{\frac{λ}{2}}$,解得λ=$\frac{2}{3}$.
∴$\overrightarrow{CG}$=$\overrightarrow{BG}$-$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{{e}_{1}}$-$\frac{2}{3}$$\overrightarrow{{e}_{2}}$,
∴$\overrightarrow{CF}$=$\overrightarrow{BF}-\overrightarrow{BC}$=$\frac{3}{2}$($\frac{1}{3}$$\overrightarrow{{e}_{1}}$-$\frac{2}{3}$$\overrightarrow{{e}_{2}}$)=$\frac{3}{2}$$\overrightarrow{CG}$.
∴CG与CF共线,G在CF上,
∴三角形三条中线交与一点.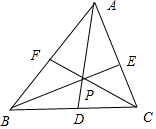
(2)证明:设D、E、F分别为BC、AC、AB的中点,
①若P是△ABC的重心,∴AP=2PD,即$\overrightarrow{PA}$=-2$\overrightarrow{PD}$,
又D是BC的中点,∴$\overrightarrow{PB}+\overrightarrow{PC}$=2$\overrightarrow{PD}$,
∴$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}$=$\overrightarrow{0}$.
②若$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}$=$\overrightarrow{0}$,则$\overrightarrow{PB}+\overrightarrow{PC}$=-$\overrightarrow{PA}$.
又D是BC的中点,∴$\overrightarrow{PB}+\overrightarrow{PC}$=2$\overrightarrow{PD}$,
∴$\overrightarrow{PA}=-2\overrightarrow{PD}$,即P在中线AD上,
同理可证P在中线BE上,P在CF上,
∴P是三角形的重心.
综上,P是△ABC重心的充要条件是$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$.
点评 本题考查了平面向量在几何证明中的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2-i}{10}$ | B. | $\frac{1+i}{10}$ | C. | $\frac{4+7i}{10}$ | D. | $\frac{4-i}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{4}{9}$) | B. | [0,$\frac{1}{3}$) | C. | (-2,0) | D. | ($\frac{1}{3}$,$\frac{4}{9}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $1+\frac{1}{2}$ | C. | $1+\frac{1}{2}+\frac{1}{3}$ | D. | $1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在(0,$\frac{π}{4}$)上单调递减 | B. | f(x)在($\frac{π}{8}$,$\frac{3π}{8}$)上单调递减 | ||
| C. | f(x)在(0,$\frac{π}{4}$)上单调递增 | D. | f(x)在($\frac{π}{8}$,$\frac{3π}{8}$)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
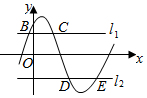 (理)如图,直线l1:y=m(0<m≤A)与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于B、C两点,直线l2:y=-m与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于D、E两点,设B(xB,yB),D(x,yD),记S(m)=|xB-xD|,则S(m)的图象大致是( )
(理)如图,直线l1:y=m(0<m≤A)与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于B、C两点,直线l2:y=-m与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于D、E两点,设B(xB,yB),D(x,yD),记S(m)=|xB-xD|,则S(m)的图象大致是( )| A. | 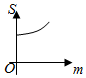 | B. | 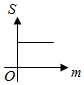 | C. | 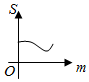 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com