Question

3．已知函数f（x）=x²-1，g（x）=x+1．
（1）求函数F（x）=f（x）+|g（x）|在区间[-2，0]上的值域．
（2）若当x∈R时，不等式f（x）≥λg（x）恒成立，求实数λ的取值范围．

Answer 1

分析 （1）画出函数F（x）的图象，结合图象求出函数的值域即可；
（2）当x∈R时，不等式f（x）≥λg（x）恒成立，可得△=λ²+4λ+4≤0，即可求实数λ的取值范围．

解答 解：（1）F（x）=x²-1+|x+1|=$\left\{\begin{array}{l}{{x}^{2}-x-2，x∈[-2，-1）}\\{{x}^{2}+1，x∈[-1，0]}\end{array}\right.$，
画出函数F（x）的图象，如图所示：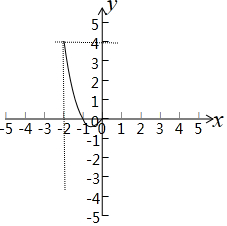
，
结合图象，x=-2时，F（x）取最大值4，
x=-$\frac{1}{2}$时，F（x）取最小值-$\frac{1}{4}$，
故函数的值域是[-$\frac{1}{4}$，4]；
（2）∵x²-1≥λ（x+1），x∈R恒成立，
∴x²-λx-λ-1≥0，x∈R恒成立，
∴△=λ²+4λ+4≤0，∴λ=-2．

点评 本题考查恒成立问题，考查函数在区间x∈[-2，0]上的最大值，考查配方法，属于中档题．