
【题目】设函数f(x)=x2+2ax﹣a﹣1,x∈[0,2],a为常数.
(1)求f(x)的最小值g(a)的解析式;
(2)在(1)中,是否存在最小的整数m,使得g(a)﹣m≤0对于任意a∈R均成立,若存在,求出m的值;若不存在,请说明理由.
【答案】
(1)解:对称轴x=﹣a
①当﹣a≤0a≥0时,
f(x)在[0,2]上是增函数,x=0时有最小值f(0)=﹣a﹣1
②当﹣a≥2a≤﹣2时,
f(x)在[0,2]上是减函数,x=2时有最小值f(2)=3a+3
③当0<﹣a<2﹣2<a<0时,
f(x)在[0,2]上是不单调,x=﹣a时有最小值f(﹣a)=﹣a2﹣a﹣1
∴ 
(2)解:存在,
由题知g(a)在 ![]() 是增函数,在
是增函数,在 ![]() 是减函数
是减函数
∴ ![]() 时,
时, ![]() ,
,
g(a)﹣m≤0恒成立
g(a)max≤m,
∴ ![]()
∵m为整数,
∴m的最小值为0
【解析】(1)由函数的解析式可得函数开口方向及对称轴,分类讨论给定区间与对称轴的关系,分析函数的单调性后,可得最值;(2)若g(a)﹣m≤0恒成立,则m不小于g(a)的最大值,分析函数g(a)的单调性求阳其最值可得答案.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
【题目】某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
| 1 | 2 | 3 | 4 | 5 |
| 1 | 4 | 5 | 6 | 6 |
(1)该同学为了求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,根据表中数据已经正确计算出
,根据表中数据已经正确计算出![]() ,试求出
,试求出![]() 的值,并估计该厂6月份生产的甲胶囊产量数;
的值,并估计该厂6月份生产的甲胶囊产量数;
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊.后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两种不同规格的产品,其质量按测试指标分数进行划分,其中分数不小于82分的为合格品,否则为次品.现随机抽取两种产品各100件进行检测,其结果如下:
测试指标分数 |
|
|
|
|
|
甲产品 | 8 | 12 | 40 | 32 | 8 |
乙产品 | 7 | 18 | 40 | 29 | 6 |
(1)根据以上数据,完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的有把握认为两种产品的质量有明显差异?
的有把握认为两种产品的质量有明显差异?
甲产品 | 乙产品 | 合计 | |
合格品 | |||
次品 | |||
合计 |
(2)已知生产1件甲产品,若为合格品,则可盈利40元,若为次品,则亏损5元;生产1件乙产品,若为合格品,则可盈利50元,若为次品,则亏损10元.记![]() 为生产1件甲产品和1件乙产品所得的总利润,求随机变量
为生产1件甲产品和1件乙产品所得的总利润,求随机变量![]() 的分布列和数学期望(将产品的合格率作为抽检一件这种产品为合格品的概率).
的分布列和数学期望(将产品的合格率作为抽检一件这种产品为合格品的概率).
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x<﹣4,或x>2},B={x|﹣1≤2x﹣1﹣2≤6}.
(1)求A∩B、(UA)∪(UB);
(2)若集合M={x|2k﹣1≤x≤2k+1}是集合A的子集,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品价格与该商品日需求量之间的几组对照数据如下表:

(1)求关于的线性回归方程;
(2)利用(1)中的回归方程,当价格![]() 元
元![]() 时,日需求量
时,日需求量![]() 的预测值为多少?
的预测值为多少?
参考公式:线性归回方程: ![]() ,其中
,其中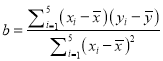 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某大学自主招生考试中,所有选报Ⅱ类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩的数据统计如下图所示,其中“数学与逻辑”科目的成绩等级为B的考生有10人.
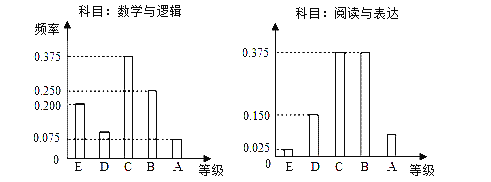
(1)求该考场考生中“阅读与表达”科目中成绩等级为A的人数;
(2)已知参加本考场测试的考生中,恰有2人的两科成绩等级均为A.在至少一科成绩等级为A的考生中,随机抽取2人进行访谈,求这2人的两科成绩等级均为A的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(1)求该单位员工当年年薪的平均值和中位数;
(2)从该单位中任取2人,此2人中年薪收入高于7万的人数记为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元,5.5万元,6万元,8.5万元,预测该员工第五年的年薪为多少?
附:线性回归方程![]() 中系数计算公式分别为:
中系数计算公式分别为:
 ,
, ![]() ,其中
,其中![]() 为样本均值.
为样本均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com